¶ 1989 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1989 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A square is cut into three rectangles along two lines parallel to a side, as shown. If the perimeter of each of the three rectangles is , then the area of the original square is
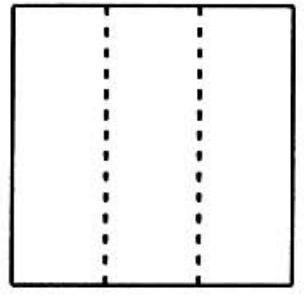
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: In the figure, is an isosceles trapezoid with side lengths , , and . The point is on and is the midpoint of hypotenuse in the right triangle . Then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Toothpicks of equal length are used to build a rectangular grid as shown. If the grid is toothpicks high and toothpicks wide, then the number of toothpicks used is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If and the triangle in the first quadrant bounded by the coordinate axes and the graph of has area , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In is an altitude, and is a median. Then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: For how many integers between and does factor into the product of two linear factors with integer coefficients?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Mr. and Mrs. Zeta want to name baby Zeta so that its monogram (first, middle, and last initials) will be in alphabetical order with no letters repeated. How many such monograms are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Consider the sequence defined recursively by (any positive number) and . For which of the following values of must
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Let and be integers with , and . If , the largest possible value for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The traffic on a certain east-west highway moves at a constant speed of miles per hour in both directions. An eastbound driver passes westbound vehicles in a five-minute interval. Assume vehicles in the westbound lane are equally spaced. Which of the following is closest to the number of westbound vehicles present in a -mile section of highway?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Two strips of width overlap at an angle of as shown. The area of the overlap (shown shaded) is
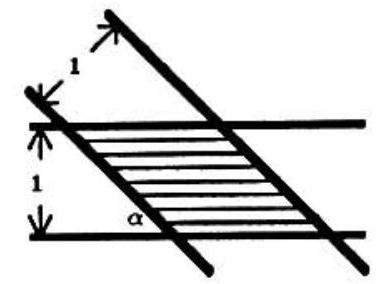
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In and is on with . Find the ratio .
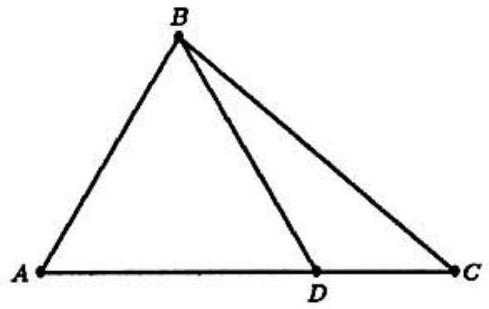
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A lattice point is a point in the plane with integer coordinates. How many lattice points are on the line segment whose endpoints are and (Include both endpoints of the segment in your count.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The perimeter of an equilateral triangle exceeds the perimeter of a square by cm. The length of each side of the triangle exceeds the length of each side of the square by . The square has perimeter greater than . How many positive integers are not possible values for
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 18: The set of all real numbers for which
is a rational number is the set of all
Answer Choices:
A. integers
B. rational
C. real
D. for which is rational
E. for which is rational
Solution:
Problem 19: A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of lengths , , and . What is the area of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be a real number selected uniformly at random between and . If , find the probability that . means the greatest integer less than or equal to .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A square flag has a red cross of uniform width with a blue square in the center on a white background as shown. (The cross is symmetric with respect to each of the diagonals of the square.) If the entire cross (both the red arms and the blue center) takes up of the area of the flag, what percent of the area of the flag is blue?
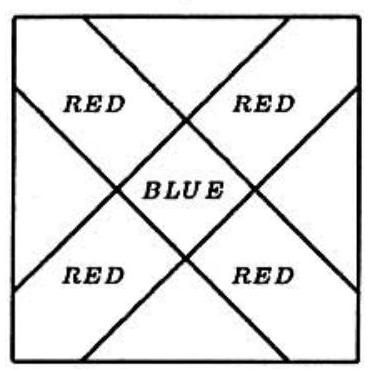
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A child has a set of distinct blocks. Each block is one of materials (plastic, wood), sizes (small, medium, large), colors (blue, green, red, yellow), and shapes (circle, hexagon, square, triangle). How many blocks in the set are different from the "plastic medium red circle" in exactly two ways? (The "wood medium red square" is such a block.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A particle moves through the first quadrant as follows. During the first minute it moves from the origin to . Thereafter, it continues to follow the directions indicated in the figure, going back and forth between the positive and axes, moving one unit of distance parallel to an axis in each minute. At which point will the particle be after exactly minutes?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Five people are sitting at a round table. Let be the number of people sitting next to at least one female and be the number of people sitting next to at least one male. The number of possible ordered pairs is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In a certain cross-country meet between two teams of five runners each, a runner who finishes in the position contributes to his team's score. The team with the lower score wins. If there are no ties among the runners, how many different winning scores are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: A regular octahedron is formed by joining the centers of adjoining faces of a cube. The ratio of the volume of the octahedron to the volume of the cube is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Let be a positive integer. If the equation has solutions in positive integers and , then must be either
Answer Choices:
A. or
B. or
C. or
D. or
E. or
Solution:
Problem 28: Find the sum of the roots of that are between and radians.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Find , where .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Suppose that boys and girls line up in a row. Let be the number of places in the row where a boy and a girl are standing next to each other. For example, for the row we have . The average value of (if all possible orders of these people are considered) is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions