¶ 1990 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1990 AHSME problems, please refer below:
Problem 1: If then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The consecutive angles of a trapezoid form an arithmetic sequence. If the smallest angle is , then the largest angle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let be a parallelogram with and . Extend through to so that . If intersects at , then is closest to
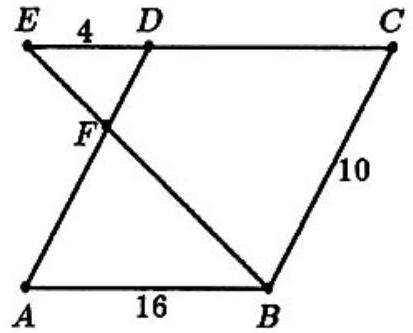
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Which of these numbers is largest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Points and are units apart. How many lines in a given plane containing and are units from and units from
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 7: A triangle with integral sides has perimeter . The area of the triangle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The number of real solutions of the equation is
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 9: Each edge of a cube is colored either red or black. Every face of the cube has at least one black edge. The smallest possible number of black edges is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: An wooden cube is formed by gluing together unit cubes. What is the greatest number of unit cubes that can be seen from a single point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many positive integers less than 50 have an odd number of positive integer divisors?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be the function defined by for some positive . If then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If the following instructions are carried out by a computer, which value of will be printed because of instruction
START AT AND at .
INCREASE THE VALUE OF BY .
INCREASE THE VALUE OF by the value .
IF IS AT LEAST , THEN GO TO INSTRUCTION ; OTHERWISE, GO TO INSTRUCTION AND PROCEED FROM THERE.
PRINT THE VALUE OF .
STOP.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: An acute isosceles triangle, , is inscribed in a circle. Through and , tangents to the circle are drawn, meeting at point . If and is the radian measure of , then
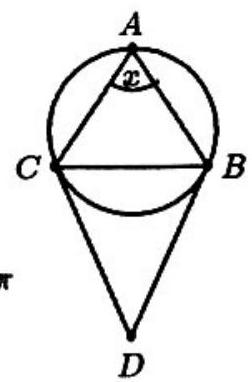
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Four whole numbers, when added three at a time, give the sums and . What is the largest of the four numbers?
Answer Choices:
A.
B.
C.
D.
E. cannot be determined from the given information
Solution:
Problem 16: At one of George Washington's parties, each man shook hands with everyone except his spouse, and no handshakes took place between women. If married couples attended, how many handshakes were there among these people?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: How many of the numbers, , have three different digits in increasing order or in decreasing order?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: First is chosen at random from the set , and then is chosen at random from the same set. The probability that the integer has units digit is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: For how many integers between and is the improper fraction not in lowest terms?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In the figure, is a quadrilateral with right angles at and . Points and are on , and and are perpendicular to . If , and , then
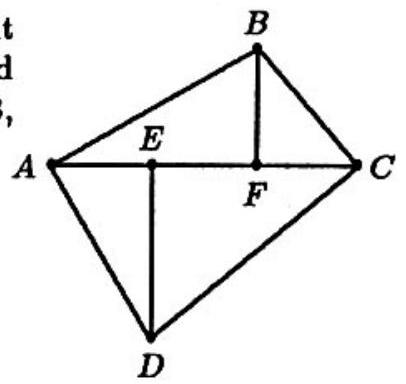
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Consider a pyramid whose base is square and whose vertex is equidistant from and . If and then the volume of the pyramid is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: If the six solutions of are written in the form , where and are real, then the product of those solutions with is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: All students at Adams High School and at Baker High School take a certain exam. The average scores for boys, for girls, and for boys and girls combined, at Adams HS and Baker HS are shown in the table, as is the average for boys at the two schools combined. What is the average score for the girls at the two schools combined?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Nine congruent spheres are packed inside a unit cube in such a way that one of them has its center at the center of the cube and each of the others is tangent to the center sphere and to three faces of the cube. What is the radius of each sphere?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Ten people form a circle. Each picks a number and tells it to the two neighbors adjacent to him in the circle. Then each person computes and announces the average of the numbers of his two neighbors. The figure shows the average announced by each person (not the original number the person picked). The number picked by the person who announced the average was
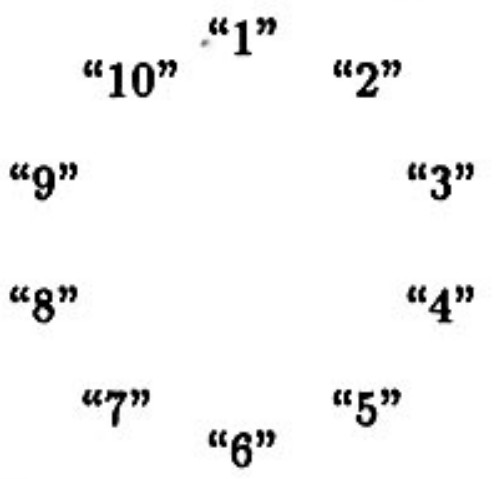
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined from the given information
Solution:
Problem 27: Which of these triples could not be the lengths of the three altitudes of a triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: A quadrilateral that has consecutive sides of lengths and is inscribed in a circle and also has a circle inscribed in it. The point of tangency of the inscribed circle to the side of length divides that side into segments of lengths and . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: A subset of the integers has the property that none of its members is times another. What is the largest number of members such a subset can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: If where , and , then is an integer. Its units digit is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions