¶ 1991 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1991 AHSME problems, please refer below:
Problem 1: If for any three distinct numbers and we define by
then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Which of the following triangles cannot exist?
Answer Choices:
A. An acute isosceles triangle
B. An isosceles right triangle
C. An obtuse right triangle
D. A scalene right triangle
E. A scalene obtuse triangle
Solution:
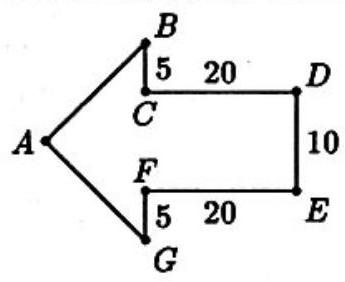
Problem 5: In the arrow-shaped polygon [see figure], the angles at vertices and are right angles, , , and . The area of the polygon is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Liquid does not mix with water. Unless obstructed, it spreads out on the surface of water to form a circular film cm thick. A rectangular box measuring cm by cm by cm is filled with liquid . Its contents are poured onto a large body of water. What will be the radius, in centimeters, of the resulting circular film?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: From time to time a population increased by , and from time to time the population increased by . Therefore, from time to time the population increased by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Point is units from the center of a circle of radius . How many different chords of the circle contain and have integer lengths?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Jack and Jill run kilometers. They start at the same point, run kilometers up a hill, and return to the starting point by the same route. Jack has a minute head start and runs at the rate of uphill and downhill. Jill runs uphill and downhill. How far from the top of the hill are they when they pass going in opposite directions?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The measures (in degrees) of the interior angles of a convex hexagon form an arithmetic sequence of positive integers. Let be the measure of the largest interior angle of the hexagon. The largest possible value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Horses and are entered in a three-horse race in which ties are not possible. If the odds against winning are -to- and the odds against winning are -to-, what are the odds against winning? (By "odds against winning are to we mean that the probability of winning the race is .)
Answer Choices:
A. -to-
B. -to-
C. -to-
D. -to-
E. -to-
Solution:
Problem 14: If is the cube of a positive integer and is the number of positive integers that are divisors of , then could be
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A circular table has exactly chairs around it. There are people seated at this table in such a way that the next person to be seated must sit next to someone. The smallest possible value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: One hundred students at Century High School participated in the last year, and their mean score was . The number of non-seniors taking the was more than the number of seniors, and the mean score of the seniors was higher than that of the non-seniors. What was the mean score of the seniors?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A positive integer is a palindrome if the integer obtained by reversing the sequence of digits of is equal to . The year is the only year in the current century with the following two properties:
It is a palindrome.
It factors as a product of a -digit prime palindrome and a -digit prime palindrome.
How many years in the millenium between and (including the year ) have properties and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: If is the set of points in the complex plane such that is a real number, then is a
Answer Choices:
A. right triangle
B. circle
C. hyperbola
D. line
E. parabola
Solution:
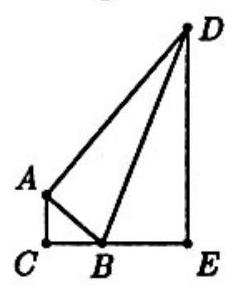
Problem 19: Triangle has a right angle at and . Triangle has a right angle at and . Points and are on opposite sides of . The line through parallel to meets extended at . If , where and are relatively prime positive integers, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The sum of all real such that is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If for all and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Two circles are externally tangent. Lines and are common tangents with and on the smaller circle and and on the larger circle. If , then the area of the smaller circle is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
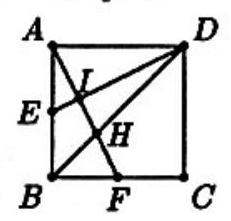
Problem 23: If is a square, is the midpoint of is the midpoint of and intersect at , and and intersect at , then the area of quadrilateral is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The graph, , of is rotated counter-clockwise about the origin to obtain a new graph . Which of the following is an equation for
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: If and
then is closest to which of the following numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: An -digit positive integer is cute if its digits are an arrangement of the set and its first digits form an integer that is divisible by , for . For example, is a cute -digit integer because divides divides , and divides . How many cute -digit integers are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: If then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Initially an urn contains black marbles and white marbles. Repeatedly, three marbles are removed from the urn and replaced from a pile outside the urn as follows:
Which of the following sets of marbles could be the contents of the urn after repeated applications of this procedure?
Answer Choices:
A. black marbles
B. white marbles
C. black marble
D. black and white marble
E. white marble
Solution:
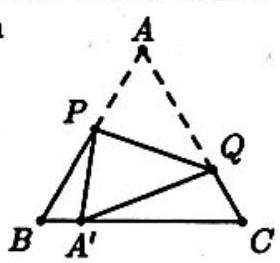
Problem 29: Equilateral triangle has been creased and folded so that vertex now rests at on as shown. If and then the length of crease is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: For any set , let denote the number of elements in , and let be the number of subsets of , including the empty set and the set itself. If and are sets for which
then what is the minimum possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions