¶ 1992 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1992 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: An urn is filled with coins and beads, all of which are either silver or gold. Twenty percent of the objects in the urn are beads. Forty percent of the coins in the urn are silver. What percent of the objects in the urn are gold coins?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If and the points and lie on a line with slope , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If and are positive integers and and are odd, then is
Answer Choices:
A. odd for all choices of
B. even for all choices of
C. odd, if is even; even, if is odd
D. odd, if is odd; even, if is even
E. odd, if is not a multiple of ; even, if is a multiple of
Solution:
Problem 6: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The ratio of to is , of to is and of to is . What is the ratio of to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A square floor is tiled with congruent square tiles. The tiles on the two diagonals of the floor are black. The rest of the tiles are white. If there are black tiles, then the total number of tiles is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Five equilateral triangles, each with side , are arranged so they are all on the same side of a line containing one side of each. Along this line, the midpoint of the base of one triangle is a vertex of the next. The area of the region of the plane that is covered by the union of the five triangular regions is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The number of positive integers for which the equation has an integer solution for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The ratio of the radii of two concentric circles is . If is a diameter of the larger circle, is a chord of the larger circle that is tangent to the smaller circle, and , then the radius of the larger circle is
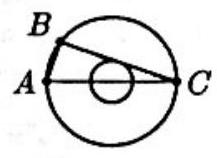
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be the image when the line is reflected across the -axis. The value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many pairs of positive integers with satisfy the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Which of the following equations have the same graph?
Answer Choices:
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
E. None. All the equations have different graphs
Solution:
Problem 15: Let . Define a sequence of complex numbers by for . In the complex plane, how far from the origin is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If for three positive numbers and , all different, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The two-digit integers from to are written consecutively to form the large integer
If is the highest power of that is a factor of , then
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 18: The increasing sequence of positive integers has the property that for all . If , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: For each vertex of a solid cube, consider the tetrahedron determined by the vertex and the midpoints of the three edges that meet at that vertex. The portion of the cube that remains when these eight tetrahedra are cut away is called a cuboctahedron. The ratio of the volume of the cuboctahedron to the volume of the original cube is closest to which of these?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Part of an "-pointed regular star" is shown. It is a simple closed polygon in which all edges are congruent, angles , are congruent and angles are congruent. If the acute angle at is less than the acute angle at , then
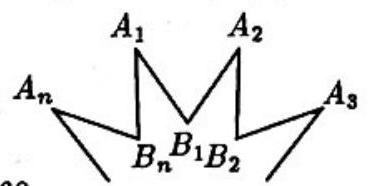
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: For a finite sequence of numbers, the Cesàro sum of is defined to be
where . If the Cesàro sum of the -term sequence is , what is the Cesàro sum of the -term sequence
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Ten points are selected on the positive -axis, , and five points are selected on the positive -axis, . The fifty segments connecting the ten selected points on to the five selected points on are drawn. What is the maximum possible number of points of intersection of these fifty segments that could lie in the interior of the first quadrant?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: What is the size of the largest subset, , of such that no pair of distinct elements of has a sum divisible by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let be a parallelogram of area 10 with and . Locate and on segments and , respectively, with . Let the line through parallel to intersect at . The area of the quadrilateral is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In triangle and . If perpendiculars constructed to at and to at meet at , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Semicircle has center and radius . Point is on such that . Extend and to points and , respectively, such that the circular arcs and have centers at and , respectively. Circular arc has center . The area of the shaded "smile" region, denoted by , is
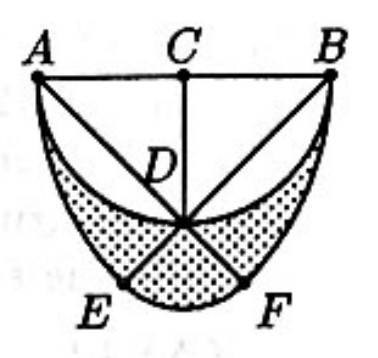
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A circle of radius has chords of length and of length . When and are extended through and , respectively, they intersect at , which is outside the circle. If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Let . The product of the real parts of the roots of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: An "unfair" coin has a probability of turning up heads. If this coin is tossed times, what is the probability that the total number of heads is even?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Let be an isosceles trapezoid with bases and . Suppose and a circle with center on is tangent to segments and . If is the smallest possible value of , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions