¶ 1993 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1993 AHSME problems, please refer below:
Problem 1: For integers and , define to mean . Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In is on side and is on side . If , then
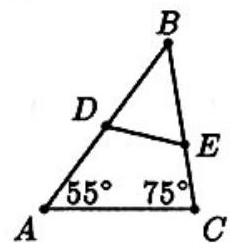
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Define the operation "" by , for all real numbers and . For how many real numbers does
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 5: Last year a bicycle cost and a cycling helmet cost . This year the cost of the bicycle increased by , and the cost of the helmet increased by . The percent increase in the combined cost of the bicycle and the helmet is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The symbol stands for an integer whose base-ten representation is a sequence of ones. For example, , etc. When is divided by , the quotient is an integer whose base-ten representation is a sequence containing only ones and zeros. The number of zeros in is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let and be circles of radius that are in the same plane and tangent to each other. How many circles of radius are in this plane and tangent to both and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Country has of the world's population and owns of the world's wealth. Country has of the world's population and of its wealth. Assume that the citizens of share the wealth of equally, and assume that those of share the wealth of equally. Find the ratio of the wealth of a citizen of to the wealth of a citizen of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Let be the number that results when both the base and the exponent of are tripled, where . If equals the product of and where , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: If , then how many digits are in the base-ten representation for
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If for all , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A square of perimeter is inscribed in a square of perimeter . What is the greatest distance between a vertex of the inner square and a vertex of the outer square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The convex pentagon has and . What is the area of
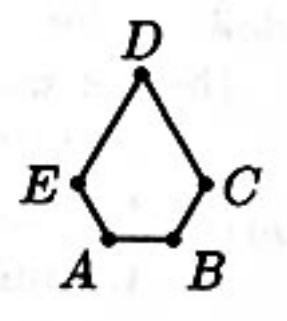
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: For how many values of will an -sided regular polygon have interior angles with integral degree measures?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Consider the non-decreasing sequence of positive integers
in which the positive integer appears times. The remainder when the term is divided by is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Amy painted a dart board over a square clock face using the "hour positions" as boundaries. If is the area of one of the eight triangular regions such as that between o'clock and o'clock, and is the area of one of the four corner quadrilaterals such as that between o'clock and o'clock, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Al and Barb start their new jobs on the same day. Al's schedule is workdays followed by rest-day. Barb's schedule is work-days followed by rest-days. On how many of their first days do both have rest-days on the same day?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: How many ordered pairs of positive integers are solutions to
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 20: Consider the equation , where is a complex variable and . Which of the following statements is true?
Answer Choices:
A. For all positive real numbers , both roots are pure imaginary.
B. For all negative real numbers , both roots are pure imaginary.
C. For all pure imaginary numbers , both roots are real and rational.
D. For all pure imaginary numbers , both roots are real and irrational.
E. For all complex numbers , neither root is real.
Solution:
Problem 21: Let be a finite arithmetic sequence with
If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Twenty cubical blocks are arranged as shown. First, are arranged in a triangular pattern; then a layer of , arranged in a triangular pattern, is centered on the ; then a layer of , arranged in a triangular pattern, is centered on the ; and finally one block is centered on top of the third layer. The blocks in the bottom layer are numbered through in some order. Each block in layers and is assigned the number which is the sum of the numbers assigned to the three blocks on which it rests. Find the smallest possible number which could be assigned to the top block.
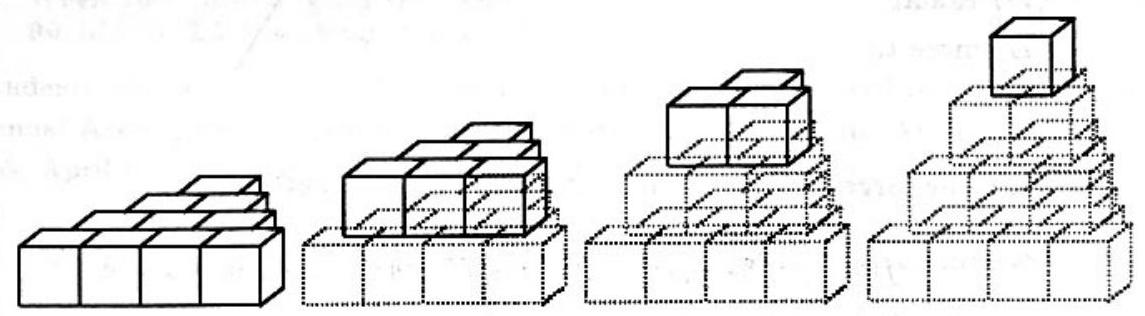
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Points and are on a circle of diameter , and is on diameter . If and , then
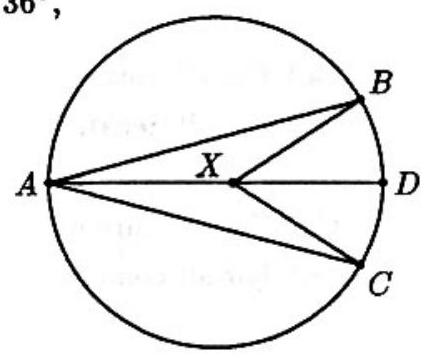
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A box contains shiny pennies and dull pennies. One by one, pennies are drawn at random from the box and not replaced. If the probability is that it will take more than four draws until the third shiny penny appears and is in lowest terms, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be the set of points on the rays forming the sides of a angle, and let be a fixed point inside the angle on the angle bisector. Consider all distinct equilateral triangles with and in . (Points and may be on the same ray, and switching the names of and does not create a distinct triangle.) There are
.jpg)
Answer Choices:
A. exactly such triangles.
B. exactly such triangles.
C. exactly such triangles.
D. exactly such triangles.
E. more than such triangles.
Solution:
Problem 26: Find the largest positive value attained by the function
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: The sides of have lengths and . A circle with center and radius rolls around the inside of , always remaining tangent to at least one side of the triangle. When first returns to its original position, through what distance has traveled?
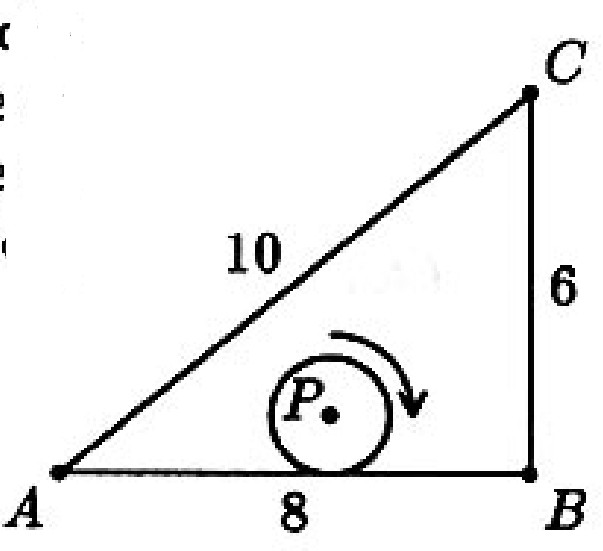
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: How many triangles with positive area are there whose vertices are points in the -plane whose coordinates are integers satisfying and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Which of the following sets could NOT be the lengths of the external diagonals of a right rectangular prism [a "box"]? (An external diagonal is a diagonal of one of the rectangular faces of the box.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Given , let
for all integers . For how many is it true that
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions