¶ 1994 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1994 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A large rectangle is partitioned into four rectangles by two segments parallel to its sides. The areas of three of the resulting rectangles are shown. What is the area of the fourth rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many of the following are equal to for all
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: In the -plane, the segment with endpoints and is the diameter of a circle. If the point is on the circle, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Pat intended to multiply a number by but instead divided by . Pat then meant to add but instead subtracted . After these mistakes, the result was . If the correct operations had been used, the value produced would have been
Answer Choices:
A. less than
B. between and
C. between and
D. between and
E. greater than
Solution:
Problem 6: In the sequence
each term is the sum of the two terms to its left. Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Squares and are congruent, , and is the center of square . The area of the region in the plane covered by these squares is
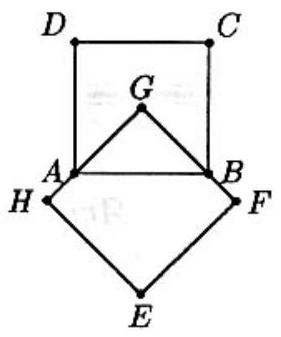
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: In the polygon shown, each side is perpendicular to its adjacent sides, and all of the sides are congruent. The perimeter of the polygon is . The area of the region bounded by the polygon is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: If is four times , and the complement of is four times the complement of , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: For distinct real numbers and , let be the larger of and and let be the smaller of and . If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Three cubes of volume and are glued together at their faces. The smallest possible surface area of the resulting configuration is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In triangle . If there is a point strictly between and such that , then
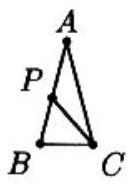
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Find the sum of the arithmetic series
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: For how many in is the tens digit of odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Some marbles in a bag are red and the rest are blue. If one red marble is removed, then one-seventh of the remaining marbles are red. If two blue marbles are removed instead of one red, then one-fifth of the remaining marbles are red. How many marbles were in the bag originally?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: An by rectangle has the same center as a circle of radius . The area of the region common to both the rectangle and the circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Triangle is inscribed in a circle, and . If and are adjacent vertices of a regular polygon of sides inscribed in this circle, then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Label one disk "", two disks "", three disks "", ..., fifty disks "". Put these labeled disks in a box. Disks are then drawn from the box at random without replacement. The minimum number of disks that must be drawn to guarantee drawing at least ten disks with the same label is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose is a geometric sequence with common ratio and . If is an arithmetic sequence, then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Find the number of counterexamples to the statement:
"If is an odd positive integer the sum of whose digits is and none of whose digits is , then is prime."
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Nine chairs in a row are to be occupied by six students and Professors Alpha, Beta and Gamma. These three professors arrive before the six students and decide to choose their chairs so that each professor will be between two students. In how many ways can Professors Alpha, Beta and Gamma choose their chairs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: In the -plane, consider the -shaped region bounded by horizontal and vertical segments with vertices at , and . The slope of the line through the origin that divides the area of this region exactly in half is
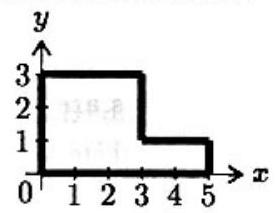
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A sample consisting of five observations has an arithmetic mean of and a median of . The smallest value that the range (largest observation minus smallest) can assume for such a sample is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: If and are non-zero real numbers such that
then the integer nearest to is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: A regular polygon of sides is exactly enclosed (no overlaps, no gaps) by regular polygons of sides each. (Shown here for .) If , what is the value of
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A bag of popping corn contains white kernels and yellow kernels. Only of the white kernels will pop, whereas of the yellow ones will pop. A kernel is selected at random from the bag, and pops when placed in the popper. What is the probability that the kernel selected was white?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: In the -plane, how many lines whose -intercept is a positive prime number and whose -intercept is a positive integer pass through the point
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Points and on a circle of radius are situated so that , and the length of minor arc is . If angles are measured in radians, then
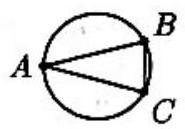
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: When standard -sided dice are rolled, the probability of obtaining a sum of is greater than zero and is the same as the probability of obtaining a sum of . The smallest possible value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions