¶ 1995 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1995 AHSME problems, please refer below:
Problem 1: Kim earned scores of and on her first three mathematics examinations. If Kim receives a on the fourth exam, then her average will
Answer Choices:
A. remain the same
B. increase by
C. increase by
D. increase by
E. increase by
Solution:
Problem 2: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The total in-store price for an appliance is . A television commercial advertises the same product for three easy payments of and a onetime shipping & handling charge of . How much is saved by buying the appliance from the television advertiser?
Answer Choices:
A. cents
B. cents
C. cents
D. cents
E. cents
Solution:
Problem 4: If is of is of , and is of , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A rectangular field is feet wide and feet long. Random sampling indicates that there are, on the average, three ants per square inch throughout the field. [ inches foot.] Of the following, the number that most closely approximates the number of ants in the field is
Answer Choices:
A. thousand
B. million
C. million
D. million
E. billion
Solution:
Problem 6: The figure shown can be folded into the shape of a cube. In the resulting cube, which of the lettered faces is opposite the face marked
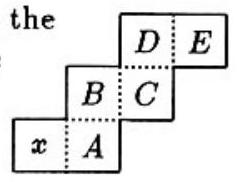
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The radius of Earth at the equator is approximately miles. Suppose a jet flies once around Earth at a speed of miles per hour relative to Earth. If the flight path is a negligible height above the equator, then, among the following choices, the best estimate of the number of hours of flight is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: In triangle and . Points and are on and , respectively, and . If , then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Consider the figure consisting of a square, its diagonals, and the segments joining the midpoints of opposite sides. The total number of triangles of any size in the figure is
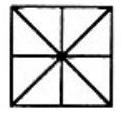
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The area of the triangle bounded by the lines and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many four-digit numbers, , satisfy all three of the following conditions?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be a linear function with the properties that , and . Which of the following statements is true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The addition below is incorrect. The display can be made correct by changing one digit , wherever it occurs, to another digit . Find the sum of and .
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 14: If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Five points on a circle are numbered , and in clockwise order. A bug jumps in a clockwise direction from one point to another around the circle; if it is on an odd-numbered point, it moves one point, and if it is on an even-numbered point, it moves two points. If the bug begins on point , after jumps it will be on point
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Anita attends a baseball game in Atlanta and estimates that there are fans in attendance. Bob attends a baseball game in Boston and estimates that there are in attendance. A league official who knows the actual numbers attending the two games notes that:
The actual attendance in Atlanta is within of Anita's estimate.
Bob's estimate is within of the actual attendance in Boston.
To the nearest , the largest possible difference between the numbers attending the two games is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Given regular pentagon , a circle can be drawn that is tangent to at and to at . The number of degrees in minor arc is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Two rays with common endpoint form a angle. Point lies on one ray, point on the other ray, and . The maximum possible length of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Equilateral triangle is inscribed in equilateral triangle as shown with . The ratio of the area of to the area of is
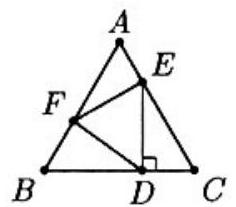
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If and are three (not necessarily different) numbers chosen randomly and with replacement from the set , the probability that is even is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two nonadjacent vertices of a rectangle are and , and the coordinates of the other two vertices are integers. The number of such rectangles is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A pentagon is formed by cutting a triangular corner from a rectangular piece of paper. The five sides of the pentagon have lengths and , although this is not necessarily their order around the pentagon. The area of the pentagon is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The sides of a triangle have lengths , and , where is an integer. For how many values of is the triangle obtuse?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: There exist positive integers and , with no common factor greater than , such that
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A list of five positive integers has mean and range . The mode and median are both . How many different values are possible for the second largest element of the list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: In the figure, and are diameters of the circle with center , , and chord intersects at . If and , then the area of the circle is
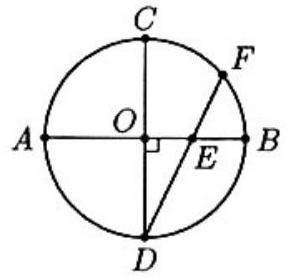
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Consider the triangular array of numbers with along the sides and interior numbers obtained by adding the two adjacent numbers in the previous row. Rows through are shown.
.jpg)
Let denote the sum of the numbers in row . What is the remainder when is divided by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Two parallel chords in a circle have lengths and , and the distance between them is . The chord parallel to these chords and midway between them is of length where is
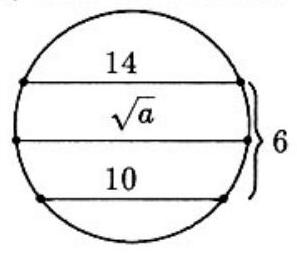
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: For how many three-element sets of positive integers is it true that
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: A large cube is formed by stacking unit cubes. A plane is perpendicular to one of the internal diagonals of the large cube and bisects that diagonal. The number of unit cubes that the plane intersects is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions