¶ 1996 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1996 AHSME problems, please refer below:
Problem 1: The addition below is incorrect. What is the largest digit that can be changed to make the addition correct?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Each day Walter gets for doing his chores or for doing them exceptionally well. After days of doing his chores daily, Walter has received a total of . On how many days did Walter do them exceptionally well?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Six numbers from a list of nine integers are , and . The largest possible value of the median of all nine numbers in this list is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Given that , which of the following is the largest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A father takes his twins and a younger child out to dinner on the twins' birthday. The restaurant charges for the father and for each year of a child's age, where age is defined as the age at the most recent birthday. If the bill is , which of the following could be the age of the youngest child?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Triangle and square are in perpendicular planes. Given that , and , what is
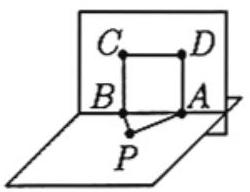
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many line segments have both their endpoints located at the vertices of a given cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Given a circle of radius , there are many line segments of length that are tangent to the circle at their midpoints. Find the area of the region consisting of all such line segments.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A function from the integers to the integers is defined as follows:
Suppose is odd and . What is the sum of the digits of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Sunny runs at a steady rate, and Moonbeam runs times as fast, where is a number greater than . If Moonbeam gives Sunny a head start of meters, how many meters must Moonbeam run to overtake Sunny?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let denote the sum of the even digits of . For example, . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Two opposite sides of a rectangle are each divided into congruent segments, and the endpoints of one segment are joined to the center to form triangle . The other sides are each divided into congruent segments, and the endpoints of one of these segments are joined to the center to form triangle . [See figure for .] What is the ratio of the area of triangle to the area of triangle
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A fair standard six-sided die is tossed three times. Given that the sum of the first two tosses equals the third, what is the probability that at least one "" is tossed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In rectangle , angle is trisected by and , where is on is on , and . Which of the following is closest to the area of the rectangle
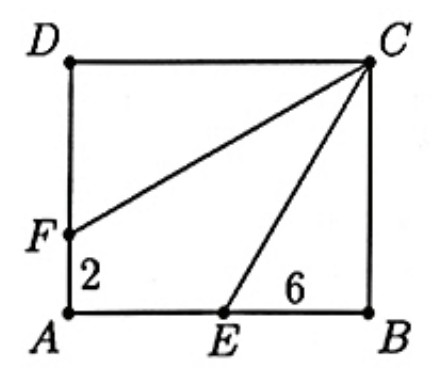
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A circle of radius has center at . A circle of radius has center at . A line is tangent to the two circles at points in the first quadrant. Which of the following is closest to the -intercept of the line?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The midpoints of the sides of a regular hexagon are joined to form a smaller hexagon. What fraction of the area of is enclosed by the smaller hexagon?
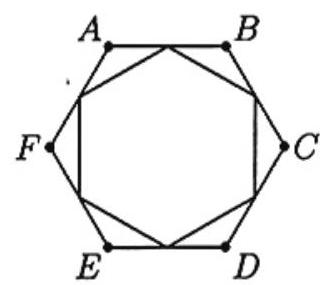
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In the -plane, what is the length of the shortest path from to that does not go inside the circle
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Triangles and are isosceles with , and intersects at . If , then is
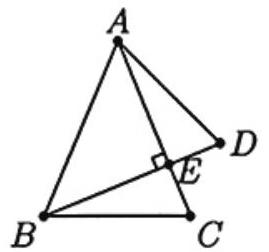
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 22: Four distinct points, , and , are to be selected from points evenly spaced around a circle. All quadruples are equally likely to be chosen. What is the probability that the chord intersects the chord
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The sum of the lengths of the twelve edges of a rectangular box is , and the distance from one corner of the box to the farthest corner is . The total surface area of the box is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The sequence
consists of 's separated by blocks of 's with 's in the block. The sum of the first terms of this sequence is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Given that , what is the largest possible value that can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: An urn contains marbles of four colors: red, white, blue, and green. When four marbles are drawn without replacement, the following events are equally likely:
the selection of four red marbles;
the selection of one white and three red marbles;
the selection of one white, one blue, and two red marbles; and
the selection of one marble of each color.
What is the smallest number of marbles satisfying the given condition?
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 27: Consider two solid spherical balls, one centered at with radius , and the other centered at with radius . How many points with only integer coordinates (lattice points) are there in the intersection of the balls?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: On a rectangular parallelepiped, vertices , and are adjacent to vertex . The perpendicular distance from to the plane containing , and is closest to
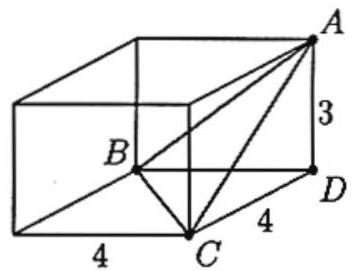
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: If is a positive integer such that has positive divisors and has positive divisors, then how many positive divisors does have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: A hexagon inscribed in a circle has three consecutive sides each of length and three consecutive sides each of length . The chord of the circle that divides the hexagon into two trapezoids, one with three sides each of length and the other with three sides each of length , has length equal to , where and are relatively prime positive integers. Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions