¶ 1984 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1984 AIME problems here.
Discussion Forum
Engage in discussion about the 1984 AIME math contest by visiting Random Math AIME 1984 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1984 AIME problems, please refer below:
Problem 1: Find the value of if is an arithmetic progression with common difference , and .
Solution:
Problem 2: The integer is the smallest positive multiple of such that every digit of is either or . Compute .
Solution:
Problem 3: A point is chosen in the interior of so that when lines are drawn through parallel to the sides of , the resulting smaller triangles, and in the figure, have areas and , respectively. Find the area of .
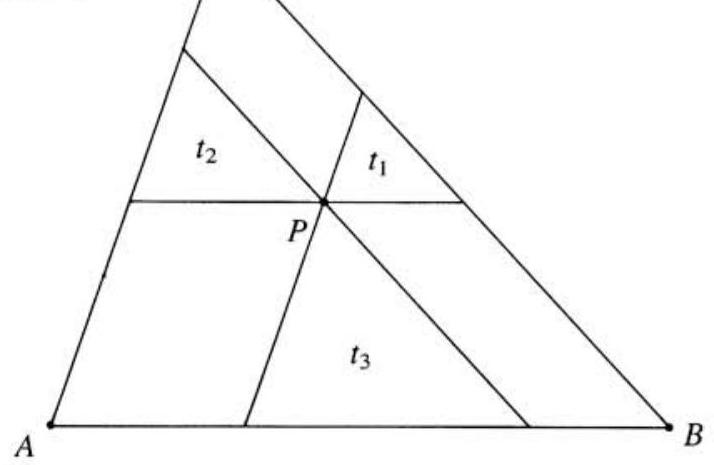
Solution:
Problem 4: Let be a list of positive integers - not necessarily distinct-in which the number appears. The average (arithmetic mean) of the numbers in is . However, if is removed, the average of the remaining numbers drops to . What is the largest number that can appear in
Solution:
Problem 5: Determine the value of if and .
Solution:
Problem 6: Three circles, each of radius , are drawn with centers at and . A line passing through is such that the total area of the parts of the three circles to one side of the line is equal to the total area of the parts of the three circles to the other side of it. What is the absolute value of the slope of this line?
Solution:
Problem 7: The function is defined on the set of integers and satisfies
Find .
Solution:
Problem 8: The equation has one complex root with argument (angle) between and in the complex plane. Determine the degree measure of .
Solution:
Problem 9: In tetrahedron , edge has length . The area of face is and the area of face is . These two faces meet each other at a angle. Find the volume of the tetrahedron in .
Solution:
Problem 10: Mary told John her score on the American High School Mathematics Examination (AHSME), which was over . From this, John was able to determine the number of problems Mary solved correctly. If Mary's score had been any lower, but still over , John could not have determined this. What was Mary's score? (Recall that the AHSME consists of multiple-choice problems and that one's score, , is computed by the formula , where is the number of correct and is the number of wrong answers; students are not penalized for problems left unanswered.)
Solution:
Problem 11: A gardener plants three maple trees, four oak trees and five birch trees in a row. He plants them in random order, each arrangement being equally likely. Let in lowest terms be the probability that no two birch trees are next to one another. Find .
Solution:
Problem 12: A function is defined for all real numbers and satisfies
for all real . If is a root of , what is the least number of roots must have in the interval
Solution:
Problem 13: Find the value of .
Solution:
Problem 14: What is the largest even integer which cannot be written as the sum of two odd composite numbers? (Recall that a positive integer is said to be composite if it is divisible by at least one positive integer other than and itself.)
Solution:
Problem 15: Determine if
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions