¶ 1983 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1983 AIME problems here.
Discussion Forum
Engage in discussion about the 1983 AIME math contest by visiting Random Math AIME 1983 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1983 AIME problems, please refer below:
Problem 1: Let and all exceed and let be a positive number such that
Find .
Solution:
Problem 2: Let , where . Determine the minimum value taken by for in the interval .
Solution:
Problem 3: What is the product of the real roots of the equation
Solution:
Problem 4: A machine-shop cutting tool has the shape of a notched circle, as shown. The radius of the circle is , the length of is and that of is . The angle is a right angle. Find the square of the distance (in centimeters) from to the center of the circle.
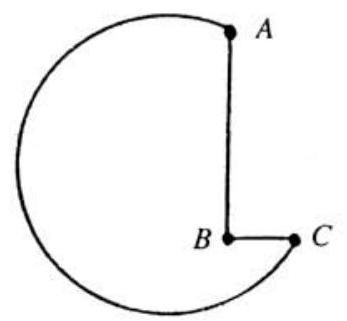
Solution:
Problem 5: Suppose that the sum of the squares of two complex numbers and is and the sum of their cubes is . What is the largest real value that can have?
Solution:
Problem 6: Let . Determine the remainder on dividing by .
Solution:
Problem 7: Twenty five of King Arthur's knights are seated at their customary round table. Three of them are chosen - all choices of three being equally likely - and are sent off to slay a troublesome dragon. Let be the probability that at least two of the three had been sitting next to each other. If is written as a fraction in lowest terms, what is the sum of the numerator and denominator?
Solution:
Problem 8: What is the largest -digit prime factor of the integer
Solution:
Problem 9: Find the minimum value of
for .
Solution:
Problem 10: The numbers and have something in common: each is a -digit number beginning with that has exactly two identical digits. How many such numbers are there?
Solution:
Problem 11: The solid shown has a square base of side length . The upper edge is parallel to the base and has length . All other edges have length . Given that , what is the volume of the solid?
.jpg)
Solution:
Problem 12: Diameter of a circle has length a -digit integer (base ten). Reversing the digits gives the length of the perpendicular chord . The distance from their intersection point to the center is a positive rational number. Determine the length of .
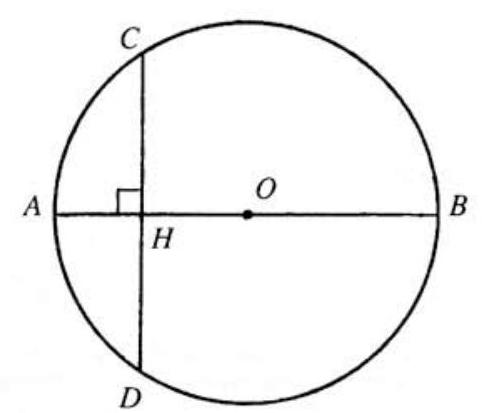
Solution:
Problem 13: For and each of its nonempty subsets a unique alternating sum is defined as follows: Arrange the numbers in the subset in decreasing order and then, beginning with the largest, alternately add and subtract successive numbers. (For example, the alternating sum for is and for it is simply .) Find the sum of all such alternating sums for .
Solution:
Problem 14: In the adjoining figure, two circles of radii and are drawn with their centers units apart. At , one of the points of intersection, a line is drawn in such a way that the chords and have equal length. Find the square of the length of .
.jpg)
Solution:
Problem 15: The adjoining figure shows two intersecting chords in a circle, with on minor arc . Suppose that the radius of the circle is , that , and that is bisected by . Suppose further that is the only chord starting at which is bisected by . It follows that the sine of the central angle of minor arc is a rational number. If this number is expressed as a fraction in lowest terms, what is the product
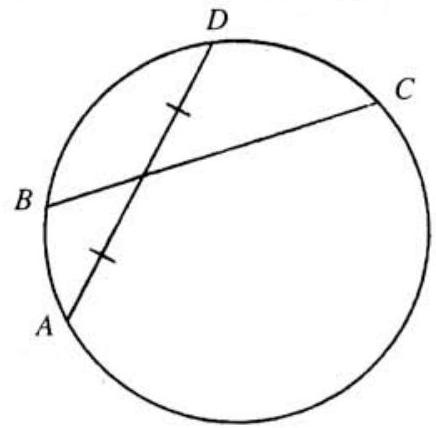
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions