¶ 2023 AMC12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2023 AMC12B problems here.
Discussion Forum
Engage in discussion about the 2023 AMC12B math contest by visiting Random Math AMC12B 2023 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2023 AMC12B problems, please refer below:
Problem 1: Mrs. Jones is pouring orange juice into four identical glasses for her four sons. She fills the first three glasses completely but runs out of juice when the fourth glass is only full. What fraction of a glass must Mrs. Jones pour from each of the first three glasses into the fourth glass so that all four glasses will have the same amount of juice?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Carlos went to a sports store to buy running shoes. Running shoes were on sale, with prices reduced by on every pair of shoes. Carlos also knew that he had to pay a sales tax on the discounted price. He had . What is the original (before discount) price of the most expensive shoes he could afford to buy?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A right triangle is inscribed in circle , and a right triangle is inscribed in circle . What is the ratio of the area of circle to the area of circle ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Jackson's paintbrush makes a narrow strip with a width of millimeters. Jackson has enough paint to make a strip meters long. How many square centimeters of paper could Jackson cover with paint?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: You are playing a game. A rectangle covers two adjacent squares (oriented either horizontally or vertically) of a grid of squares, but you are not told which two squares are covered. Your goal is to find at least one square that is covered by the rectangle. A "turn" consists of you guessing a square, after which you are told whether that square is covered by the hidden rectangle. What is the minimum number of turns you need to ensure that at least one of your guessed squares is covered by the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: When the roots of the polynomial
are removed from the real number line, what remains is the union of disjoint open intervals. On how many of these intervals is positive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: For how many integers does the expression
represent a real number, where log denotes the base logarithm?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: How many nonempty subsets of have the property that the number of elements in is equal to the least element of ? For example, satisfies the condition.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: What is the area of the region in the coordinate plane defined by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In the -plane, a circle of radius with center on the positive axis is tangent to the -axis at the origin, and a circle of radius with center on the positive -axis is tangent to the -axis at the origin. What is the slope of the line passing through the two points at which these circles intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: What is the maximum area of an isosceles trapezoid that has legs of length and one base twice as long as the other?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For complex numbers and (where ), define the binary operation
Suppose is a complex number such that . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A rectangular box has distinct edge lengths , and . The sum of the lengths of all edges of is the sum of the areas of all faces of is , and the volume of is . What is the length of the longest interior diagonal connecting two vertices of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: For how many ordered pairs of integers does the polynomial have distinct integer roots?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Suppose that , and are positive integers such that
Which of the following statements are necessarily true?
. If or or both, then .
. If , then or or both.
. if and only if and .
Answer Choices:
A. , and
B. only
C. and only
D. only
E. and only
Solution:
Problem 16: In the state of Coinland, coins have values of and cents. Suppose is the value in cents of the most expensive item in Coinland that cannot be purchased using these coins with exact change. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The three side lengths of a triangle are in arithmetic progression with shortest side of length One of the interior angles measures . What is the area of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Last academic year Yolanda and Zelda took different courses that did not necessarily administer the same number of quizzes during each of the two semesters. Yolanda's average on all the quizzes she took during the first semester was points higher than Zelda's average on all the quizzes she took during the first semester. Yolanda's average on all the quizzes she took during the second semester was points higher than her average for the first semester and was again points higher than Zelda's average on all the quizzes Zelda took during her second semester. Which one of the following statements cannot possibly be true?
Answer Choices:
A. Yolanda's quiz average for the academic year was points higher than Zelda's.
B. Zelda's quiz average for the academic year was higher than Yolanda's.
C. Yolanda's quiz average for the academic year was points higher than Zelda's.
D. Zelda's quiz average for the academic year equaled Yolanda's.
E. If Zelda had scored points higher on each quiz she took, then she would have had the same average for the academic year as Yolanda.
Solution:
Problem 19: Each of balls is randomly placed into one of bins. Which of the following is closest to the probability that each of the bins will contain an odd number of balls?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Cyrus the frog sits on a flat surface. He jumps, landing feet away. He then chooses a direction at random and again jumps feet. What is the probability that after the second jump Cyrus lands within foot of his starting position?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A lampshade is made in the form of the lateral surface of the frustum of a right circular cone. The height of the frustum is inches, its top diameter is inches, and its bottom diameter is inches. A bug is at the bottom of the lampshade and there is a glob of honey on the top edge of the lampshade at the spot farthest from the bug. The bug wants to crawl to the honey, but it must stay on the surface of the lampshade. What is the length in inches of its shortest path to the honey?
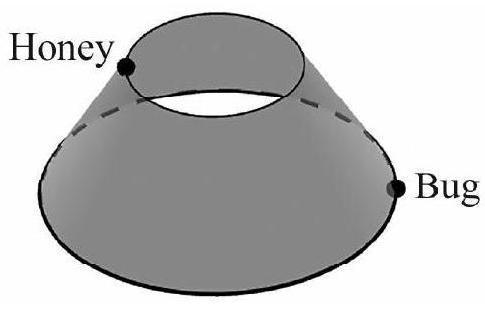
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A real-valued function has the property that for all real numbers and ,
Which one of the following cannot be the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: When a standard -sided die is rolled times, the product of the numbers rolled can be any of possible values. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Suppose that , and are positive integers satisfying all of the following relations.
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A regular pentagon with area is printed on paper and cut out. All five vertices are folded to the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions