¶ 2024 AMC12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2024 AMC12B problems here.
Discussion Forum
Engage in discussion about the 2024 AMC12B math contest by visiting Random Math AMC12B 2024 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2024 AMC12B problems, please refer below:
Problem 1: In a long line of people arranged left to right, the 1013 th person from the left is also the 1010th person from the right. How many people are in the line?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: For how many integer values of is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Balls numbered are deposited in 5 bins, labeled , and E , using the following procedure. Ball 1 is deposited in bin A, and balls 2 and 3 are deposited in bin B . The next 3 balls are deposited in bin C , the next 4 in bin D , and so on, cycling back to bin A after balls are deposited in bin E. (For example, balls numbered are deposited in bin B at step 7 of this process.) In which bin is ball 2024 deposited?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In the following expression, Melanie changed some of the plus signs to minus signs:
When the new expression was evaluated, it was negative. What is the least number of plus signs that Melanie could have changed to minus signs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The national debt of the United States is on track to reach dollars by 2033. How many digits does this number of dollars have when written as a numeral in base 5 ? (The approximation of as 0.7 is sufficient for this problem.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
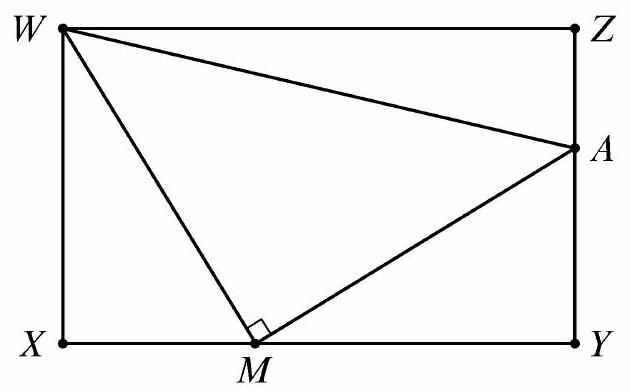
Problem 7: In the figure below is a rectangle with and . Point lies on , point lies on , and is a right angle. The areas of triangles and are equal. What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: What value of satisfies
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A dartboard is the region in the coordinate plane consisting of points such that . A target is the region where . A dart is thrown and lands at a random point in . The probability that the dart lands in can be expressed as , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A list of 9 real numbers consists of , and 7 , as well as , and with . The range of the list is 7 , and the mean and the median are both positive integers. How many ordered triples are possible?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 11: Let . What is the mean of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Suppose is a complex number with positive imaginary part, with real part greater than 1 , and with . In the complex plane, the four values , and are the vertices of a quadrilateral with area 15 . What is the imaginary part of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: There are real numbers , and that satisfy the system of equations
What is the minimum possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: How many different remainders can result when the 100 th power of an integer is divided by 125 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A triangle in the coordinate plane has vertices , and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A group of 16 people will be partitioned into 4 indistinguishable 4-person committees. Each committee will have one chairperson and one secretary. The number of different ways to make these assignments can be written as , where and are positive integers and is not divisible by 3 . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Integers and are randomly chosen without replacement from the set of integers with absolute value not exceeding 10 . What is the probability that the polynomial has 3 distinct integer roots?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The Fibonacci numbers are defined by , and for . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
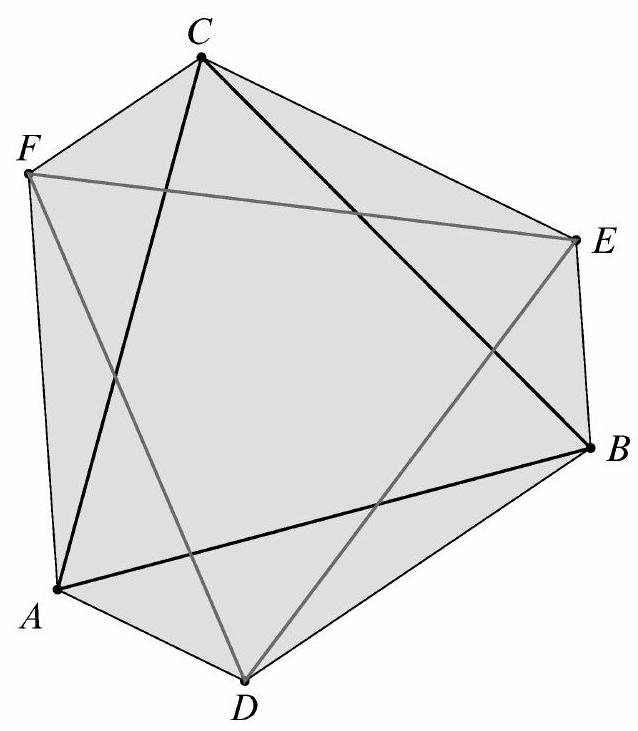
Problem 19: Equilateral with side length 14 is rotated about its center by angle , where , to form . See the figure. The area of hexagon is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose , and are points in the plane with and , and let be the length of the line segment from to the midpoint of . Define a function by letting be the area of . Then the domain of is an open interval , and the maximum value of occurs at . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The measures of the smallest angles of three different right triangles sum to . All three triangles have side lengths that are primitive Pythagorean triples. Two of them are 3-4-5 and 5-12-13. What is the perimeter of the third triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be a triangle with integer side lengths and the property that . What is the least possible perimeter of such a triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A right pyramid has regular octagon with side length 1 as its base and apex . Segments and are perpendicular. What is the square of the height of the pyramid?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: What is the number of ordered triples of positive integers, with , such that there exists a (non-degenerate) triangle with an integer inradius for which , and are the lengths of the altitudes from to to , and to , respectively? (Recall that the inradius of a triangle is the radius of the largest possible circle that can be inscribed in the triangle.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Pablo will decorate each of 6 identical white balls with either a striped or a dotted pattern, using either red or blue paint. He will decide on the color and pattern for each ball by flipping a fair coin for each of the 12 decisions he must make. After the paint dries, he will place the 6 balls in an urn. Frida will randomly select one ball from the urn and note its color and pattern. The events "the ball Frida selects is red" and "the ball Frida selects is striped" may or may not be independent, depending on the outcome of Pablo's coin flips. The probability that these two events are independent can be written as , where and are relatively prime positive integers. What is ? (Recall that two events and are independent if and .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions