¶ 2024 AMC12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2024 AMC12A problems here.
Discussion Forum
Engage in discussion about the 2024 AMC12A math contest by visiting Random Math AMC12A 2024 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2024 AMC12A problems, please refer below:
Problem 1: What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A model used to estimate the time it will take to hike to the top of a mountain on a trail is of the form , where and are constants, is the time in minutes, is the length of the trail in miles, and is the altitude gain in feet. The model estimates that it will take 69 minutes to hike to the top if a trail is 1.5 miles long and ascends 800 feet, as well as if a trail is 1.2 miles long and ascends 1100 feet. How many minutes does the model estimate it will take to hike to the top if the trail is 4.2 miles long and ascends 4000 feet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The number 2024 is written as the sum of not necessarily distinct two-digit numbers. What is the least number of two-digit numbers needed to write this sum?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the least value of such that ! is a multiple of 2024 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A data set containing 20 numbers, some of which are 6 , has mean 45 . When all the 6 s are removed, the data set has mean 66 . How many 6 s were in the original data set?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The product of three integers is 60 . What is the least possible positive sum of the three integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In and . Points lie on hypotenuse so that . What is the length of the vector sum
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: How many angles with satisfy ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Let be the greatest integer such that both and are perfect squares. What is the units digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Let be the radian measure of the smallest angle in a right triangle. Let be the radian measure of the smallest angle in a 7-24-25 right triangle. In terms of , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: There are exactly positive integers with such that the base- integer is divisible by 16 (where 16 is in base ten). What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The first three terms of a geometric sequence are the integers , and , where . What is the sum of the digits of the least possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The graph of has an axis of symmetry. What is the reflection of the point over this axis?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The numbers, in order, of each row and the numbers, in order, of each column of a array of integers form an arithmetic progression of length 5 . The numbers in positions , and are , and 12 , respectively. What number is in position
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The roots of are , and . What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A set of 12 tokens- 3 red, 2 white, 1 blue, and 6 black-is to be distributed at random to 3 game players, 4 tokens per player. The probability that some player gets all the red tokens, another player gets all the white tokens, and the remaining player gets the blue token can be written as , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Integers , and satisfy , and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: On top of a rectangular card with sides of length 1 and , an identical card is placed so that two of their diagonals line up, as shown ( , in this case).
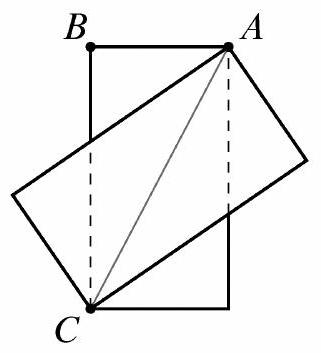
Continue the process, adding a third card to the second, and so on, lining up successive diagonals after rotating clockwise. In total, how many cards must be used until a vertex of a new card lands exactly on the vertex labeled in the figure?
Answer Choices:
A.
B.
C.
D.
E. No new vertex will land on .
Solution:
Problem 19: Cyclic quadrilateral has lengths and with . What is the length of the shorter diagonal of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Points and are chosen uniformly and independently at random on sides and , respectively, of equilateral triangle . Which of the following intervals contains the probability that the area of is less than half the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Suppose that and the sequence satisfies the recurrence relation
for all . What is the greatest integer less than or equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The figure below shows a dotted grid 8 cells wide and 3 cells tall consisting of squares. Carl places 1 -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A disphenoid is a tetrahedron whose triangular faces are congruent to one another. What is the least total surface area of a disphenoid whose faces are scalene triangles with integer side lengths?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A graph is symmetric about a line if the graph remains unchanged after reflection in that line. For how many quadruples of integers , where and and are not both 0 , is the graph of
symmetric about the line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions