¶ 2018 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2018 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2018 AMC8 math contest by visiting Random Math 2018 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2018 AMC8 problems, please refer below:
Problem 1: An amusement park has a collection of scale models, with a ratio of , of buildings and other sights from around the country. The height of the United States Capitol is feet.What is the height in feet of its replica at this park, rounded to the nearest whole number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is the value of the product
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Students Arn, Bob, Cyd, Dan, Eve, and Fon are arranged in that order in a circle. They start counting: Arn first, then Bob, and so forth. When the number contains a as a digit (such as ) or is a multiple of that person leaves the circle and the counting continues. Who is the last one present in the circle?
Answer Choices:
A. Arn
B. Bob
C. Cyd
D. Dan
E. Eve
Solution:
Problem 4: The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in
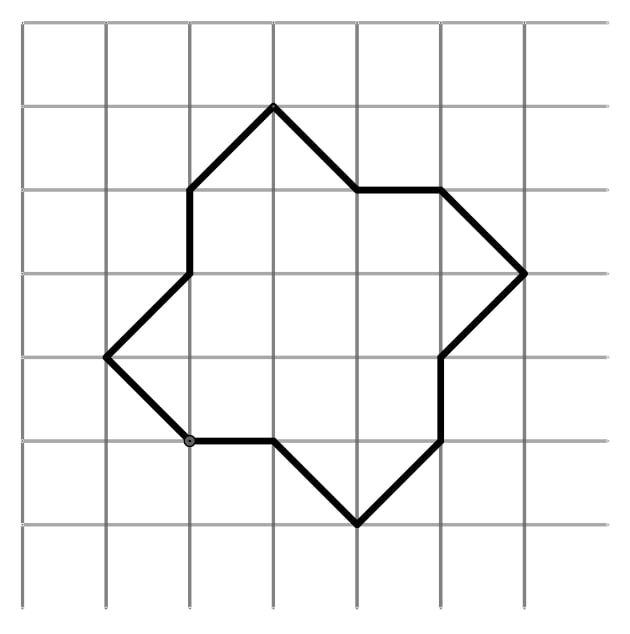
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: On a trip to the beach, Anh traveled miles on the highway and miles on a coastal access road. He drove three times as fast on the highway as on the coastal road. If Anh spent minutes driving on the coastal road, how many minutes did his entire trip take?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The -digit number is divisible by . What is the remainder when this number is divided by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Mr. Garcia asked the members of his health class how many days last week they exercised for at least minutes. The results are summarized in the following bar graph, where the heights of the bars represent the number of students. What was the mean number of days of exercise last week, rounded to the nearest hundredth, reported by the students in Mr. Garcia's class?
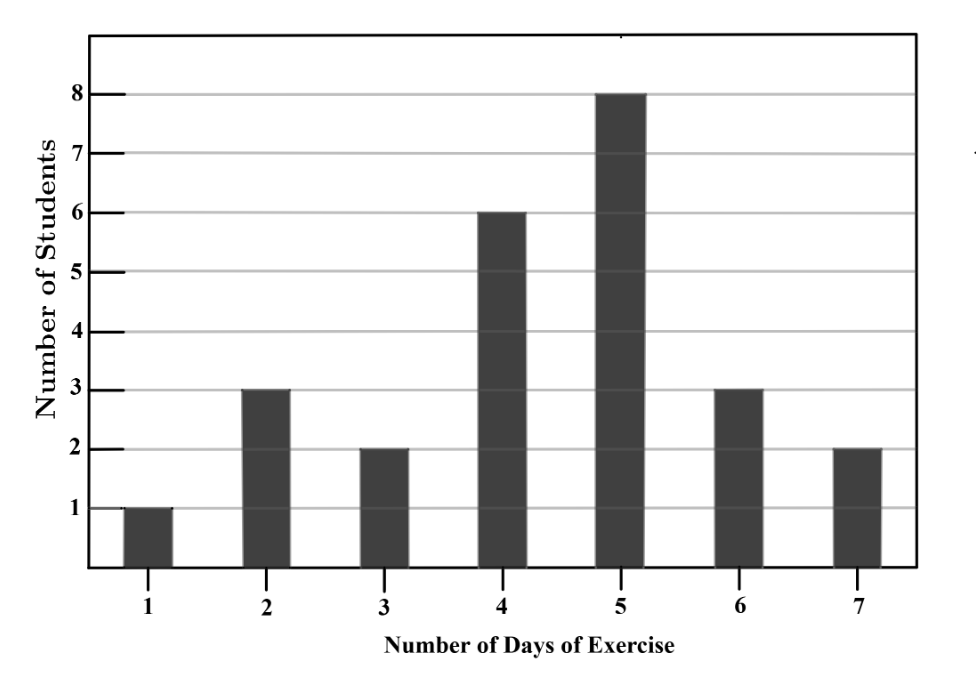
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Tyler is tiling the floor of his foot by foot living room. He plans to place one-foot by one-foot square tiles to form a border along the edges of the room and to fill in the rest of the floor with two-foot by two-foot square tiles. How many tiles will he use?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The harmonic mean of a set of non-zero numbers is the reciprocal of the average of the reciprocals of the numbers. What is the harmonic mean of and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.
If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The clock in Sri's car, which is not accurate, gains time at a constant rate. One day as he begins shopping he notes that his car clock and his watch (which is accurate) both say noon. When he is done shopping, his watch says and his car clock says . Later that day, Sri loses his watch. He looks at his car clock and it says . What is the actual time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Laila took five math tests, each worth a maximum of 100 points. Laila's score on each test was an integer between and , inclusive. Laila received the same score on the first four tests, and she received a higher score on the last test. Her average score on the five tests was . How many values are possible for Laila's score on the last test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let be the greatest five-digit number whose digits have a product of . What is the sum of the digits of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In the diagram below, the diameter of each of the two smaller circles is the radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?
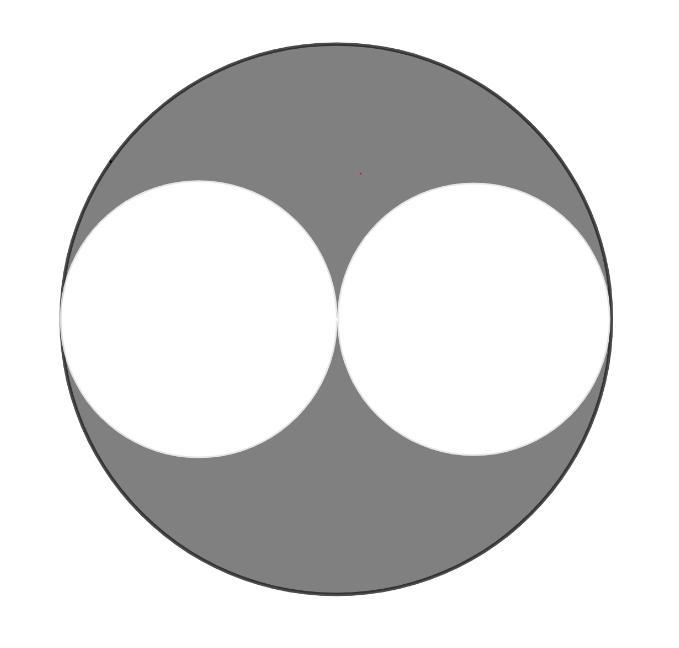
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Bella begins to walk from her house toward her friend Ella's house. At the same time, Ella begins to ride her bicycle toward Bella's house. They each maintain a constant speed, and Ella rides times as fast as Bella walks. The distance between their houses is miles, which is feet, and Bella covers feet with each step. How many steps will Bella take by the time she meets Ella?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: How many positive factors does have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In a sign pyramid a cell gets a if the two cells below it have the same sign, and it gets a if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a at the top of the pyramid?
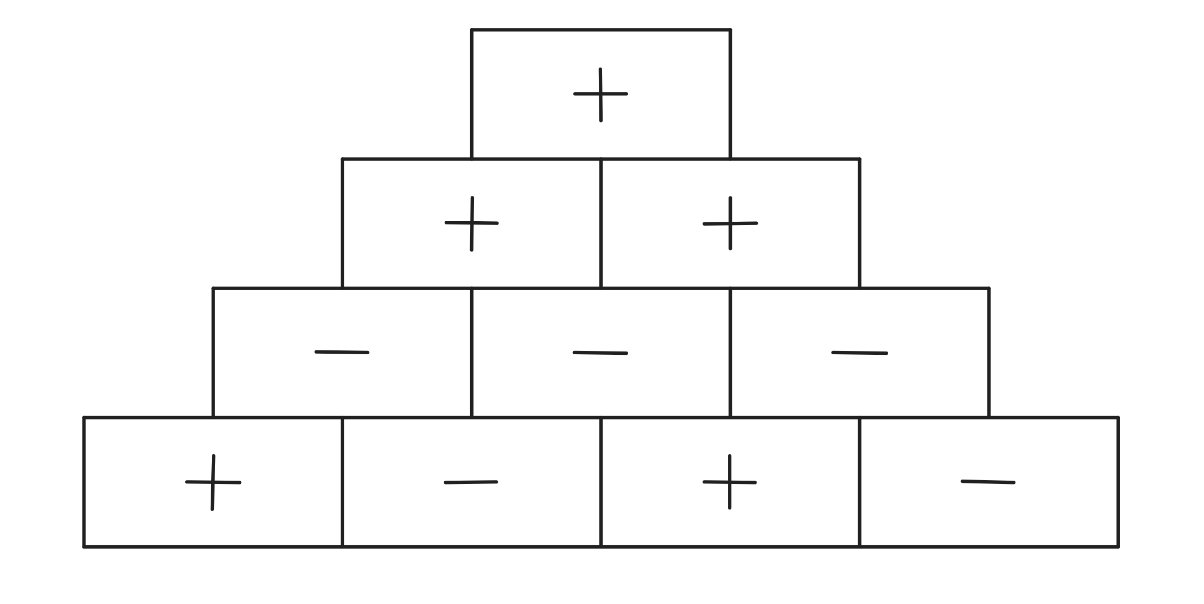
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In , a point is on such that and . Point is on so that and point is on so that . What is the ratio of the area of to the area of triangle
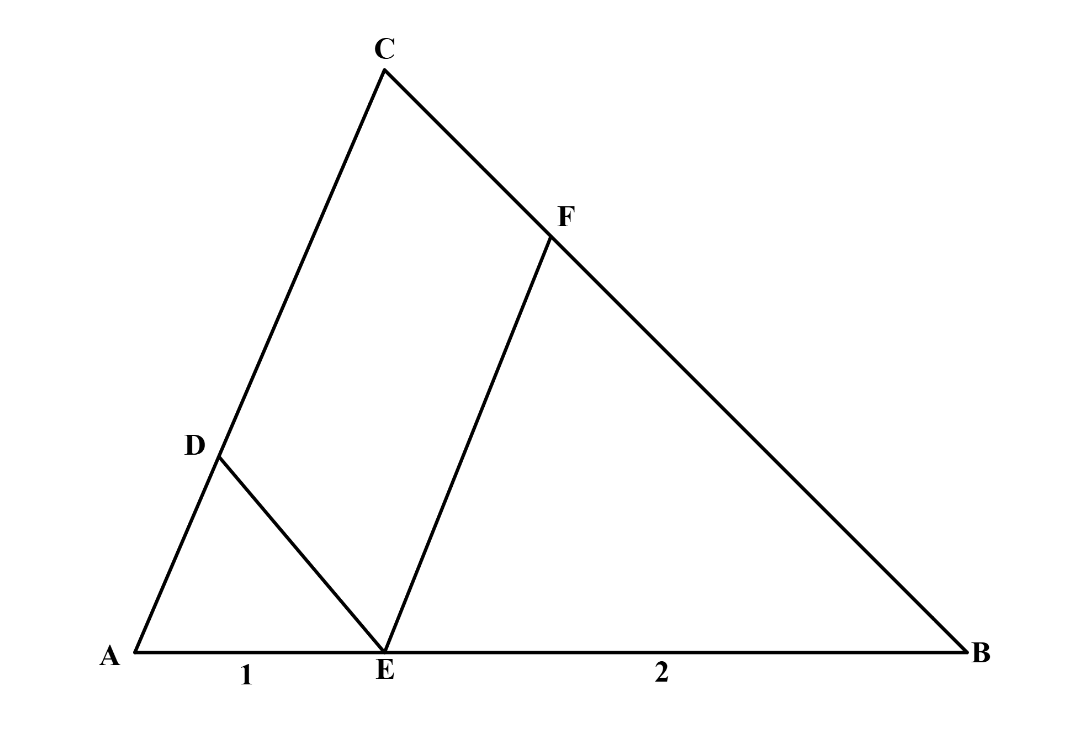
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many positive three-digit integers have a remainder of when divided by , a remainder of when divided by , and a remainder of when divided by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Point is the midpoint of side in square , and meets diagonal at . The area of quadrilateral is . What is the area of
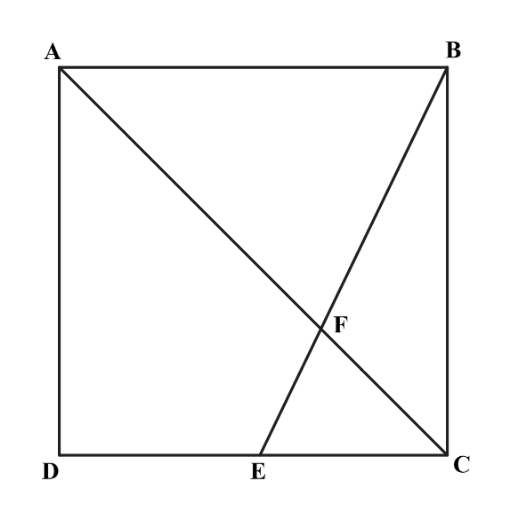
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: From a regular octagon, a triangle is formed by connecting three randomly chosen vertices of the octagon. What is the probability that at least one of the sides of the triangle is also a side of the octagon?
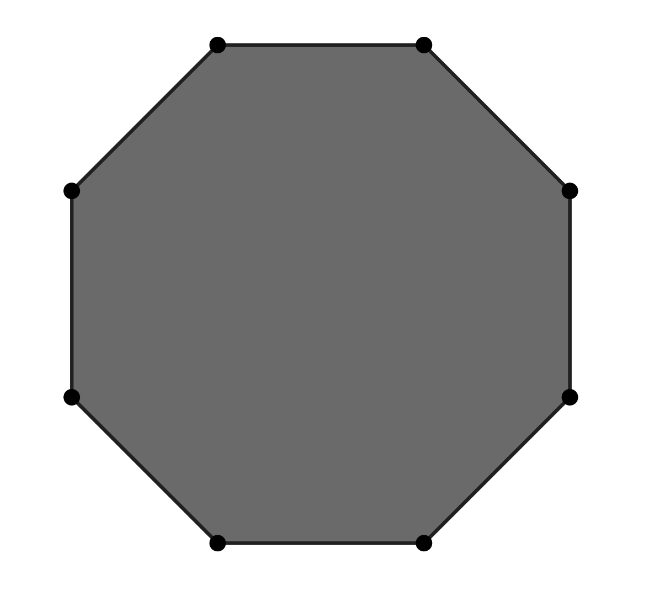
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In the cube with opposite vertices and , and are the midpoints of segments and , respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What is
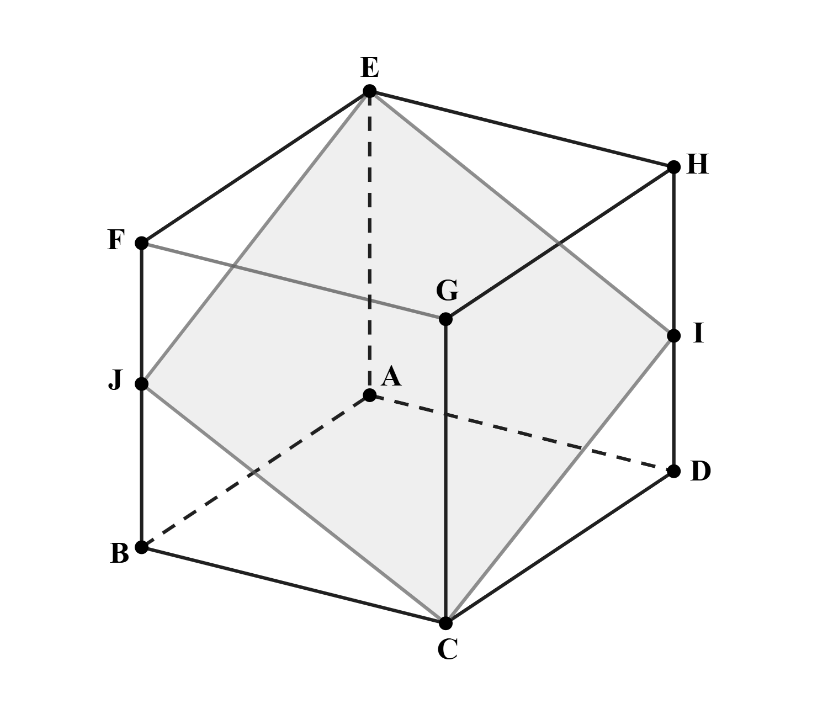
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: How many perfect cubes lie between and , inclusive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions