¶ 2023 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2023 AIME I problems here.
Discussion Forum
Engage in discussion about the 2023 AIME I math contest by visiting Random Math AIME I 2023 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2023 AIME I problems, please refer below:
Problem 1: Five men and nine women stand equally spaced around a circle in random order. The probability that every man stands diametrically opposite a woman is , where and are relatively prime positive integers. Find .
Solution:
Problem 2: Positive real numbers and satisfy the equations
The value of is , where and are relatively prime positive integers. Find .
Solution:
Problem 3: A plane contains lines, no of which are parallel. Suppose that there are points where exactly lines intersect, points where exactly lines intersect, points where exactly lines intersect, points where exactly lines intersect, and no points where more than lines intersect. Find the number of points where exactly lines intersect.
Solution:
Problem 4: The sum of all positive integers such that is a perfect square can be written as , where , and are positive integers. Find .
Solution:
Problem 5: Let be a point on the circle circumscribing square that satisfies and . Find the area of .
Solution:
Problem 6: Alice knows that red cards and black cards will be revealed to her one at a time in random order. Before each card is revealed, Alice must guess its color. If Alice plays optimally, the expected number of cards she will guess correctly is , where and are relatively prime positive integers. Find .
Solution:
Problem 7: Call a positive integer extra-distinct if the remainders when is divided by , and are distinct. Find the number of extra-distinct positive integers less than .
Solution:
Problem 8: Rhombus has . There is a point on the incircle of the rhombus such that the distances from to the lines , and are , and , respectively. Find the perimeter of .
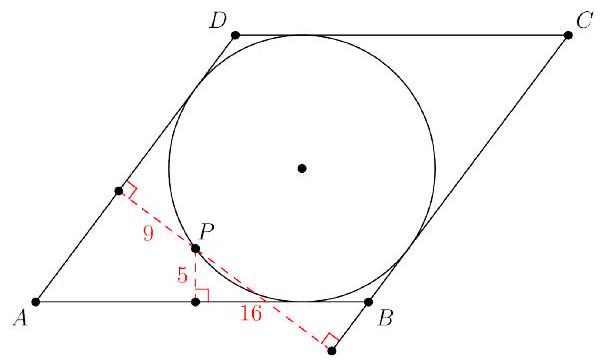
Solution:
Problem 9: Find the number of cubic polynomials , where , and are integers in , such that there is a unique integer with .
Solution:
Problem 10: There exists a unique positive integer for which the sum
is an integer strictly between and . For that unique , find . (Note that denotes the greatest integer that is less than or equal to .)
Solution:
Problem 11: Find the number of subsets of that contain exactly one pair of consecutive integers. Examples of such subsets are and .
Solution:
Problem 12: Let be an equilateral triangle with side length . Points , and lie on , and , respectively, with , and . Point inside has the property that
Find .
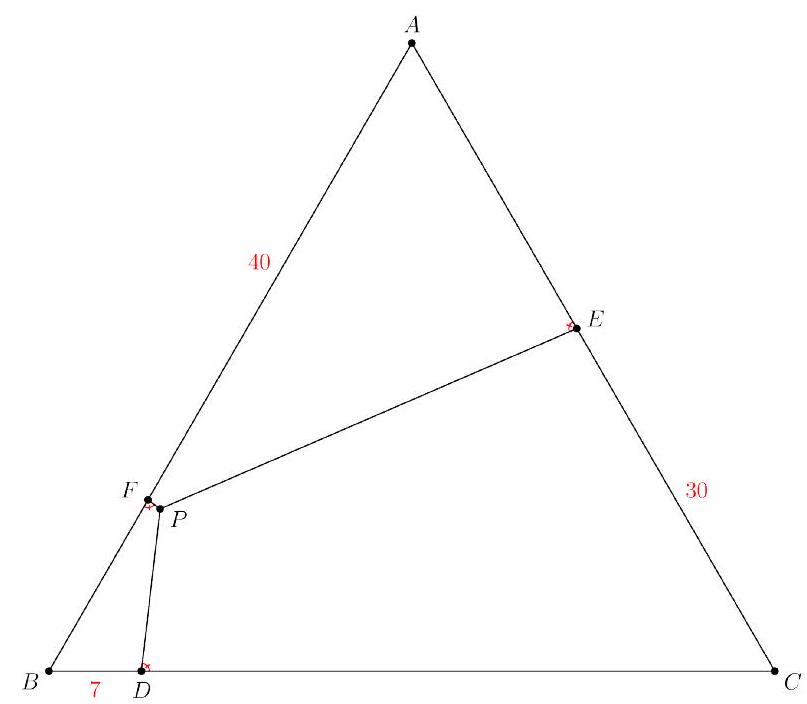
Solution:
Problem 13: Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths and . The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is , where and are relatively prime positive integers. Find . A parallelepiped is a solid with six parallelogram faces such as the one shown below.
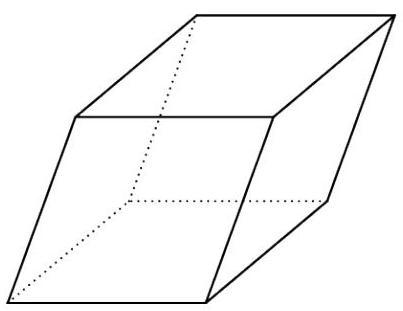
Solution:
Problem 14: The following analog clock has two hands that can move independently of each other.
Initially, both hands point to the number . The clock performs a sequence of hand movements so that on each movement, one of the two hands moves clockwise to the next number on the clock face while the other hand does not move.
Let be the number of sequences of hand movements such that during the sequence, every possible positioning of the hands appears exactly once, and at the end of the movements, the hands have returned to their initial position. Find the remainder when is divided by .
.jpg)
Solution:
Problem 15: Find the largest prime number for which there exists a complex number satisfying
- the real and imaginary part of are both integers;
- , and
- there exists a triangle whose three side lengths are , the real part of , and the imaginary part of .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions