¶ 2023 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2023 AIME II problems here.
Discussion Forum
Engage in discussion about the 2023 AIME II math contest by visiting Random Math AIME II 2023 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2023 AIME II problems, please refer below:
Problem 1: The numbers of apples growing on each of six apple trees form an arithmetic sequence where the greatest number of apples growing on any of the six trees is double the least number of apples growing on any of the six trees. The total number of apples growing on all six trees is . Find the greatest number of apples growing on any of the six trees.
Solution:
Problem 2: Recall that a palindrome is a number that reads the same forward and backward. Find the greatest integer less than that is a palindrome both when written in base ten and when written in base eight, such as .
Solution:
Problem 3: Let be an isosceles triangle with . There exists a point inside such that and . Find the area of .
.jpg)
Solution:
Problem 4: Let , and be real numbers satisfying the system of equations
Let be the set of possible values of . Find the sum of the squares of the elements of .
Solution:
Problem 5: Let be the set of all positive rational numbers such that when the two numbers and are written as fractions in lowest terms, the sum of the numerator and denominator of one fraction is the same as the sum of the numerator and denominator of the other fraction. The sum of all the elements of can be expressed in the form , where and are relatively prime positive integers. Find .
Solution:
Problem 6: Consider the L-shaped region formed by three unit squares joined at their sides, as shown below. Two points and are chosen independently and uniformly at random from inside the region. The probability that the midpoint of also lies inside this L-shaped region can be expressed as , where and are relatively prime positive integers. Find .
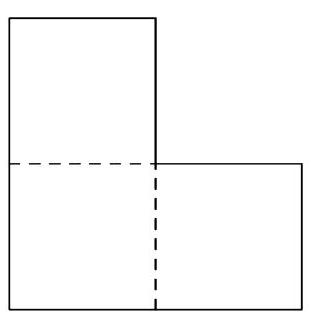
Solution:
Problem 7: Each vertex of a regular dodecagon (-gon) is to be colored either red or blue, and thus there are possible colorings. Find the number of these colorings with the property that no four vertices colored the same color are the four vertices of a rectangle.
Solution:
Problem 8: Let , where . Find the value of the product
Solution:
Problem 9: Circles and intersect at two points and , and their common tangent line closer to intersects and at points and , respectively. The line parallel to that passes through intersects and for the second time at points and , respectively. Suppose , and . Then the area of trapezoid is , where and are positive integers and is not divisible by the square of any prime. Find .
Solution:
Problem 10: Let be the number of ways to place the integers through in the cells of a grid so that for any two cells sharing a side, the difference between the numbers in those cells is not divisible by . One way to do this is shown below. Find the number of positive integer divisors of .
Solution:
Problem 11: Find the number of collections of distinct subsets of with the property that for any two subsets and in the collection, .
Solution:
Problem 12: In with side lengths , and , let be the midpoint of . Let be the point on the circumcircle of such that is on . There exists a unique point on segment such that . Then can be written as , where and are relatively prime positive integers. Find .
Solution:
Problem 13: Let be an acute angle such that . Find the number of positive integers less than or equal to such that is a positive integer whose units digit is .
Solution:
Problem 14: A cube-shaped container has vertices , and , where and are parallel edges of the cube, and and are diagonals of faces of the cube, as shown. Vertex of the cube is set on a horizontal plane so that the plane of the rectangle is perpendicular to , vertex is meters above , vertex is meters above , and vertex is meters above . The cube contains water whose surface is parallel to at a height of meters above . The volume of water is cubic meters, where and are relatively prime positive intgers. Find .
.jpg)
Solution:
Problem 15: For each positive integer let be the least positive integer multiple of such that . Find the number of positive integers less than or equal to that satisfy .
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions