¶ 2024 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2024 AIME I problems here.
Discussion Forum
Engage in discussion about the 2024 AIME I math contest by visiting Random Math AIME I 2024 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2024 AIME I problems, please refer below:
Problem 1: Every morning Aya goes for a -kilometer-long walk and stops at a coffee shop afterwards. When she walks at a constant speed of kilometers per hour, the walk takes her hours, including minutes spent in the coffee shop. When she walks at kilometers per hour, the walk takes her hours and minutes, including minutes spent in the coffee shop. Suppose Aya walks at kilometers per hour. Find the number of minutes the walk takes her, including the minutes spent in the coffee shop.
Solution:
Problem 2: There exist real numbers and , both greater than , such that . Find .
Solution:
Problem 3: Alice and Bob play the following game. A stack of tokens lies before them. The players take turns with Alice going first. On each turn, the player removes either token or tokens from the stack. Whoever removes the last token wins. Find the number of positive integers less than or equal to for which there exists a strategy for Bob that guarantees that Bob will win the game regardless of Alice's play.
Solution:
Problem 4: Jen enters a lottery by selecting four distinct elements of . Then four distinct elements of are drawn at random. Jen wins a prize if at least two of her numbers are drawn, and she wins the grand prize if all four of her numbers are drawn. The probability that Jen wins the grand prize given that Jen wins a prize is , where and are relatively prime positive integers. Find .
Solution:
Problem 5: Rectangle has dimensions and , and rectangle has dimensions and . Points and lie on line in that order, and and lie on opposite sides of line , as shown. Points and lie on a common circle. Find .
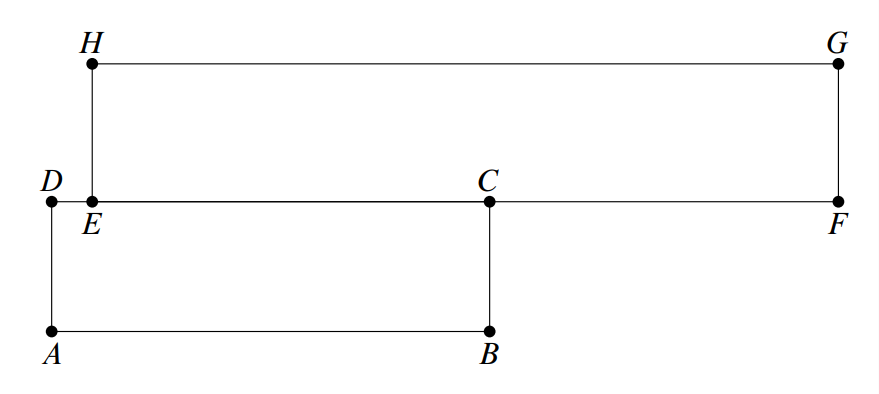
Solution:
Problem 6: Consider the paths of length that follow the lines from the lower left corner to the upper right corner on an grid. Find the number of such paths that change direction exactly four times, as in the examples shown below.
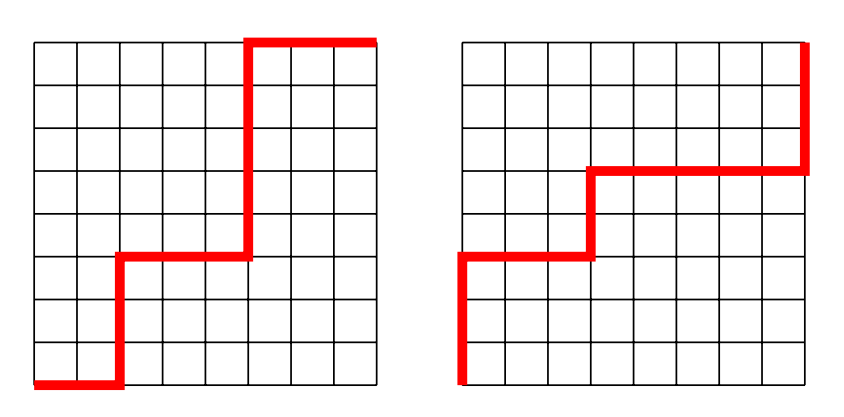
Solution:
Problem 7: Find the greatest possible real part of
where is a complex number with . Here .
Solution:
Problem 8: Eight circles of radius can be placed tangent to side of so that the circles are sequentially tangent to each other, with the first circle being tangent to and the last circle being tangent to , as shown. Similarly, circles of radius can be placed tangent to in the same manner. The inradius of can be expressed as , where and are relatively prime positive integers. Find .
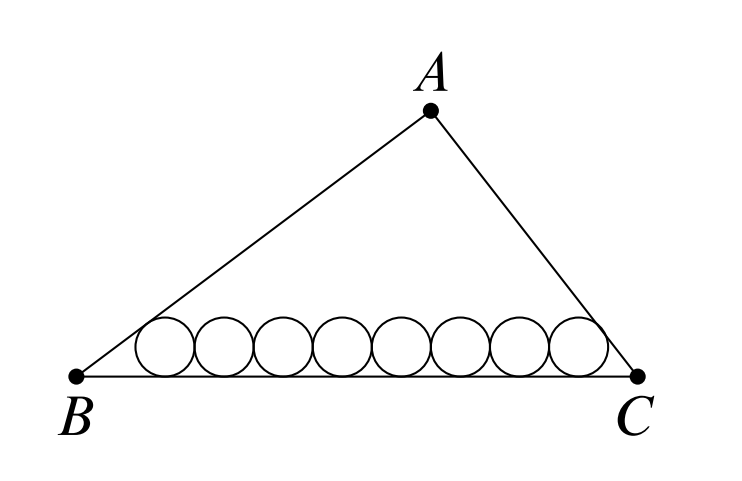
Solution:
Problem 9: Let and be points on the hyperbola such that is a rhombus whose diagonals intersect at the origin. Find the greatest real number that is less than for all such rhombi.
Solution:
Problem 10: Let have side lengths and . The tangents to the circumcircle of at and intersect at point , and intersects the circumcircle at . The length of is equal to , where and are relatively prime positive integers. Find .
Solution:
Problem 11: Each vertex of a regular octagon is independently colored either red or blue with equal probability. The probability that the octagon can then be rotated so that all of the blue vertices move to positions where there had been red vertices is , where and are relatively prime positive integers. Find .
Solution:
Problem 12: Define and . Find the number of intersections of the graphs of
Solution:
Problem 13: Let be the least prime number for which there exists an integer such that is divisible by . Find the least positive integer such that is divisible by .
Solution:
Problem 14: Let be a tetrahedron such that and . There exists a point inside the tetrahedron such that the distances from to each of the faces of the tetrahedron are all equal. This distance can be written in the form , where and are positive integers, and are relatively prime, and is not divisible by the square of any prime. Find .
Solution:
Problem 15: Let be the set of rectangular boxes with surface area and volume . Let be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of . The value of can be written as , where and are relatively prime positive integers. Find .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions