¶ 2024 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2024 AIME II problems here.
Discussion Forum
Engage in discussion about the 2024 AIME II math contest by visiting Random Math AIME II 2024 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2024 AIME II problems, please refer below:
Problem 1: Among the residents of Aimeville, there are who own a diamond ring, who own a set of golf clubs, and who own a garden spade. In addition, each of the residents owns a bag of candy hearts. There are residents who own exactly two of these things, and residents who own exactly three of these things. Find the number of residents of Aimeville who own all four of these things.
Solution:
Problem 2: A list of positive integers has the following properties:
- The sum of the items in the list is .
- The unique mode of the list is .
- The median of the list is a positive integer that does not appear in the list itself.
Find the sum of the squares of all the items in the list.
Solution:
Problem 3: Find the number of ways to place a digit in each cell of a grid so that the sum of the two numbers formed by reading left to right is , and the sum of the three numbers formed by reading top to bottom is . The grid below is an example of such an arrangement because and .
Solution:
Problem 4: Let and be positive real numbers that satisfy the following system of equations:
Then the value of is , where and are relatively prime positive integers. Find .
Solution:
Problem 5: Let be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments and has side lengths and . Find the side length of the hexagon.
Solution:
Problem 6: Alice chooses a set of positive integers. Then Bob lists all finite nonempty sets of positive integers with the property that the maximum element of belongs to . Bob's list has sets. Find the sum of the elements of .
Solution:
Problem 7: Let be the greatest four-digit positive integer with the property that whenever one of its digits is changed to , the resulting number is divisible by . Let and be the quotient and the remainder, respectively, when is divided by . Find .
Solution:
Problem 8: Torus is the surface produced by revolving a circle with radius around an axis in the plane of the circle that is a distance from the center of the circle.
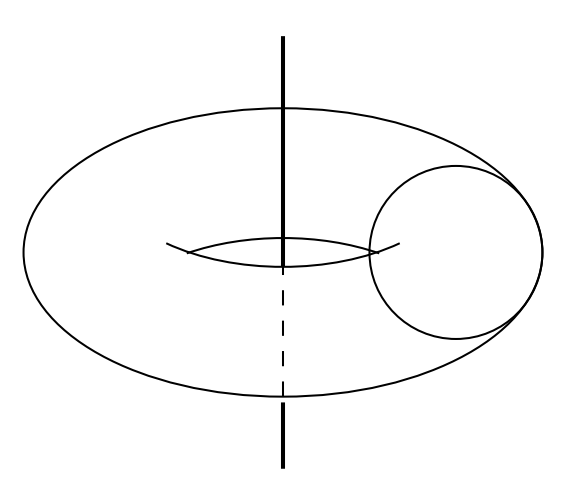
Let be a sphere with radius . When rests on the inside of , it is internally tangent to along a circle with radius , and when rests on the outside of , it is externally tangent to along a circle with radius . The difference can be written as , where and are relatively prime positive integers. Find .
Solution:
Problem 9: There is a collection of indistinguishable black chips and indistinguishable white chips. Find the number of ways to place some of these chips in unit cells of a grid so that
- each cell contains at most one chip,
- all chips in the same row and all chips in the same column have the same color, and
- any additional chip placed on the grid would violate one or more of the previous two conditions.
Solution:
Problem 10: Let have incenter , circumcenter , inradius , and circumradius . Suppose that . Find .
Solution:
Problem 11: Find the number of triples of nonnegative integers satisfying and
Solution:
Problem 12: Let and be points in the coordinate plane. Let be the family of segments of unit length lying in the first quadrant with on the -axis and on the -axis. There is a unique point on , distinct from and , that does not belong to any segment from other than . Then , where and are relatively prime positive integers. Find .
Solution:
Problem 13: Let be a th root of unity. Find the remainder when
is divided by .
Solution:
Problem 14: Let be an integer. Call a positive integer -eautiful if it has exactly two digits when expressed in base , and these two digits sum to . For example, is -eautiful because and . Find the least integer for which there are more than ten -eautiful integers.
Solution:
Problem 15: Find the number of rectangles inside a fixed regular dodecagon (-gon) where each side of the rectangle lies on a side or on a diagonal of the dodecagon. The diagram below shows three of those rectangles.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions