¶ 2025 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2025 AIME I problems here.
Discussion Forum
Engage in discussion about the 2025 AIME I math contest by visiting Random Math AIME I 2025 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2025 AIME I problems, please refer below:
Problem 1: Find the sum of all integer bases for which is a divisor of .
Solution:
Problem 2: On points and lie in that order on side with , , and . Points and lie in that order on side with , , and . Let be the reflection of through , and let be the reflection of through . Quadrilateral has area . Find the area of heptagon .
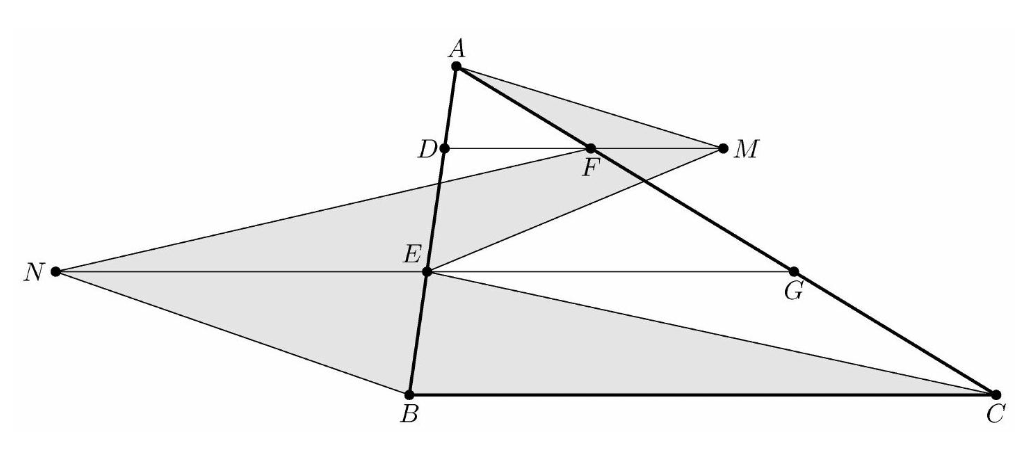
Solution:
Problem 3: The members of a baseball team went to an ice-cream parlor after their game. Each player had a singlescoop cone of chocolate, vanilla, or strawberry ice cream. At least one player chose each flavor, and the number of players who chose chocolate was greater than the number of players who chose vanilla, which was greater than the number of players who chose strawberry. Let be the number of different assignments of flavors to players that meet these conditions. Find the remainder when is divided by .
Solution:
Problem 4: Find the number of ordered pairs , where both and are integers between and , inclusive, such that .
Solution:
Problem 5: There are eight-digit positive integers that use each of the digits exactly once. Let be the number of these integers that are divisible by . Find the difference between and .
Solution:
Problem 6: An isosceles trapezoid has an inscribed circle tangent to each of its four sides. The radius of the circle is , and the area of the trapezoid is . Let the parallel sides of the trapezoid have lengths and , with . Find .
Solution:
Problem 7: The twelve letters and are randomly grouped into six pairs of letters. The two letters in each pair are placed next to each other in alphabetical order to form six two-letter words, and then those six words are listed alphabetically. For example, a possible result is . The probability that the last word listed contains is , where and are relatively prime positive integers. Find .
Solution:
Problem 8: Let be a real number such that the system
has exactly one complex solution . The sum of all possible values of can be written as , where and are relatively prime positive integers. Find . Here .
Solution:
Problem 9: The parabola with equation is rotated counterclockwise around the origin. The unique point in the fourth quadrant where the original parabola and its image intersect has -coordinate , where , , and are positive integers, and and are relatively prime. Find .
Solution:
Problem 10: The cells of a grid are filled in using the numbers through so that each row contains different numbers, and each of the three blocks heavily outlined in the example below contains different numbers, as in the first three rows of a Sudoku puzzle.
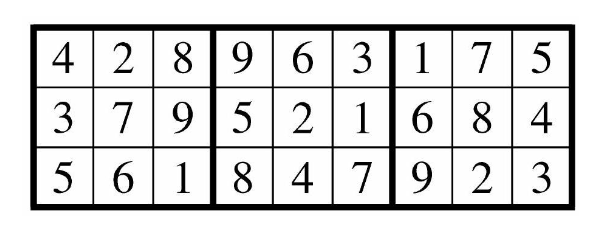
The number of different ways to fill such a grid can be written as , where and are distinct prime numbers and and are positive integers. Find .
Solution:
Problem 11: A piecewise linear periodic function is defined by
and for all real numbers . The graph of has the sawtooth pattern depicted below.
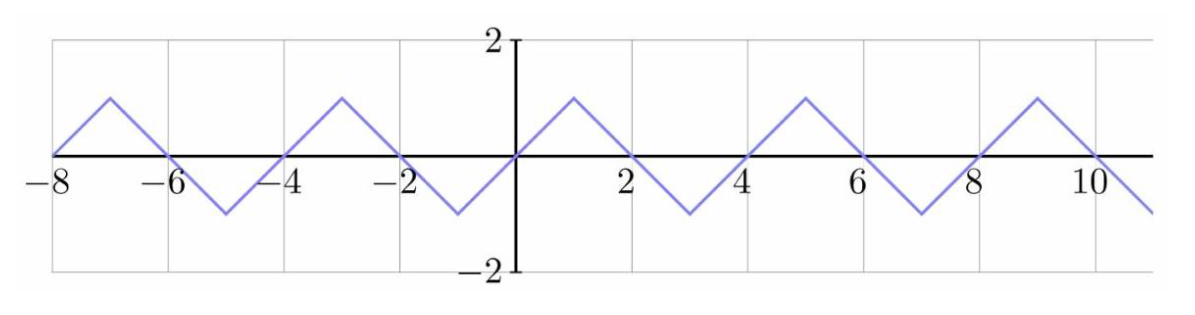
The parabola intersects the graph of at finitely many points. The sum of the -coordinates of these intersection points can be expressed in the form , where and are positive integers, and have greatest common divisor equal to , and is not divisible by the square of any prime. Find .
Solution:
Problem 12: The set of points in -dimensional coordinate space that lie in the plane whose coordinates satisfy the inequalities
forms three disjoint convex regions. Exactly one of those regions has finite area. The area of this finite region can be expressed in the form , where and are positive integers and is not divisible by the square of any prime. Find .
Solution:
Problem 13: Alex divides a disk into four quadrants with two perpendicular diameters intersecting at the center of the disk. He draws more line segments through the disk, drawing each segment by selecting two points at random on the perimeter of the disk in different quadrants and connecting those two points. Find the expected number of regions into which these line segments divide the disk.
Solution:
Problem 14: Let be a convex pentagon with , , , , , and . For each point in the plane, define . The least possible value of can be expressed as , where and are positive integers and is not divisible by the square of any prime. Find .
Solution:
Problem 15: Let denote the number of ordered triples of positive integers such that and is a multiple of . Find the remainder when is divided by .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions