¶ 1964 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1964 AHSME problems, please refer below:
Problem 1: What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The graph of is:
Answer Choices:
A. a parabola
B. an ellipse
C. a pair of straight lines
D. a point
E. none of these
Solution:
Problem 3: When a positive integer is divided by a positive integer , the quotient is and the remainder is and integers. What is the remainder when is divided by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The expression , where and , is equivalent to:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If varies directly as and if when , the value of when is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If are in geometric progression, the fourth term is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Let be the number of real values of for which the roots of are equal. Then equals:
Answer Choices:
A.
B.
C.
D. a finite number greater than 2
E. an infinitely large number
Solution:
Problem 8: The smaller root of the equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A jobber buys an article at " less ". He then wishes to sell the article at a gain of of his cost after allowing a discount on his marked price. At what price, in dollars, should the article be marked?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 10: Given a square with side of length s. On a diagonal as base a triangle with three unequal sides is constructed so that its area equals that of the square. The length of the altitude drawn to the base is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Given and ; the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Which of the following is the negation of the statement: For all of a certain set, ?
Answer Choices:
A. For all
B. For all
C. For no
D. For some
E. For some
Solution:
Problem 13: A circle is inscribed in a triangle with sides of lengths 8,13, and 17. Let the segments of the side of length 8, made by a point of tangency, be and , with . Then the ratio is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A farmer bought 749 sheep. He sold 700 of them for the price paid for the 749 sheep. The remaining 49 sheep were sold at the same price per head as the other 700. Based on the cost, the percent gain on the entire transaction is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A line through the point ( ) cuts from the second quadrant a triangular region with area . The equation of the line is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 16: Let the expression have a remainder of zero when divided by 6, and let be the set of integers . The number of members of satisfying the given condition is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Given the distinct points and . Line segments are drawn connecting these points to each other and to the origin 0. Of the three possibilities: (1) parallelogram (2) straight line (3) trapezoid, figure OPRQ, depending upon the location of the points , and , can be:
Answer Choices:
A. (1) only
B. (2) only
C. (3) only
D. (1) or (2) only
E. all three
Solution:
Problem 18: Let be the number of pairs of values of and such that and have the same graph. Then is:
Answer Choices:
A.
B.
C.
D. finite but more than 2
E. greater than any finite number
Solution:
Problem 19: If and , the numerical value of
is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The sum of the numerical coefficients of all the terms in the expansion of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Given parallelogram with the midpoint of diagonal . Point is connected to a point in DA so that . What is the ratio of the area of triangle DFE to the area of quadrilateral ABEF?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Two numbers are such that their difference, their sum, and their product are to one another as . The product of the two numbers is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let constants. For what value of is a minimum ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The set of values of for which has two factors, with integer coefficients, which are linear in and , is precisely:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: In a ten-mile race First beats Second by 2 miles and First beats Third by 4 miles. If the runners maintain constant speeds throughout the race, by how many miles does Second beat Third?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: If is a real number and where a , then:
Answer Choices:
A.
B. a
C. a
D.
E.
Solution:
Problem 28: The sum of terms of an arithmetic progression is 153 , and the common difference is 2. If the first term is an integer, and , then the number of possible values for is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: In this figure inches, 6 inches, inches, inches. The length of , in inches is:
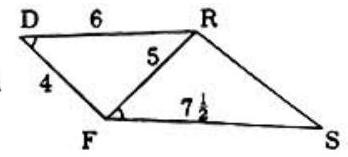
Answer Choices:
A. undetermined
B.
C.
D.
E.
Solution:
Problem 30: If , the larger root minus the smaller root is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: Let . Then , expressed in terms of , equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: If , then:
Answer Choices:
A. must equal
B. must equal zero
C. either or , or both
D. if
E.
Solution:
Problem 33: is a point interior to rectangle and such that inches, inches, and inches. Then , in inches, equals:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: If is a multiple of 4 , the sum , where , equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: The sides of a triangle are of lengths 13,14 , and 15 . The altitudes of the triangle meet at point . If is the altitude to side of length 14 , the ratio is :
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: In this figure the radius of the circle is equal to the altitude of the equilateral triangle ABC . The circle is made to roll along the side AB , remaining tangent to it at a variable point T and intersecting sides AC and in variable points and , respectively.
.jpg)
Let be the number of degrees in arc MTN. Then , for all permissible positions of the circle:
Answer Choices:
A. varies from 30 to 90
B. varies from 30 to 60
C. varies from 60 to 90
D. remains constant at 30
E. remains constant at 60
Solution:
Problem 37: Given two positive numbers such that . Let A.M. be their arithmetic mean and let G.M. be their positive geometric mean. Then A.M. minus G.M. is always less than:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: The sides and of triangle are respectively of lengths 4 inches and 7 inches. The median is inches. Then , in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 39: The magnitudes of the sides of triangle ABC are , and c , as shown, with . Through interior point and the vertices lines are drawn meeting the opposite sides in , respectively. Let . Then, for all positions of point is less than:
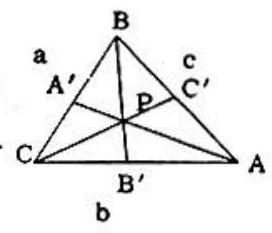
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: A watch loses minutes per day. It is set right at 1 P.M. on March 15. When the watch shows 9 A.M. on March 21, the positive correction to be added to the time shown by the watch, in minutes, equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions