¶ 1965 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1965 AHSME problems, please refer below:
Problem 1: The number of real values of satisfying the equation is:
Answer Choices:
A.
B.
C.
D.
E. more than 4
Solution:
Problem 2: A regular hexagon is inscribed in a circle. The ratio of the length of a side of the hexagon to the length of the shorter of the arcs intercepted by the side, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The expression has the same value as:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Line intersects line and line is parallel to . The three lines are distinct and lie in a plane. The number of points equidistant from all three lines is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: When the repeating decimal 0.363636 . . is written in simplest fractional form, the sum of the numerator and denominator is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The sum of the reciprocals of the roots of the equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: One side of a given triangle is 18 inches. Inside the triangle a line segment is drawn parallel to this side forming a trapezoid whose area is one-third of that of the triangle. The length of this segment, in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The vertex of the parabola will be a point on the -axis if the value of c is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The statement is equivalent to the statement:
Answer Choices:
A.
B.
C.
D. and
E. or
Solution:
Problem 11: Consider the statements: I: , II: , and III: . Of these the following are incorrect:
Answer Choices:
A.
B. I only
C. II only
D. III only
E. I and III only
Solution:
Problem 12: A rhombus is inscribed in triangle in such a way that one of its vertices is A and two of its sides lie along AB and AC . If inches, inches, and inches, the side of the rhombus, in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Let be the number of number-pairs ( ) which satisfy and . Then n is:
Answer Choices:
A.
B.
C.
D. more than two, but finite
E. greater than any finite number
Solution:
Problem 14: The sum of the numerical coefficients in the complete expansion of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The symbol represents a two-digit number in the base b . If the number is double the number , then b is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let line AC be perpendicular to line CE . Connect A to D , the midpoint of CE and connect E to B , the midpoint of AC . If AD and EB intersect in point F , and inches, then the area of triangle DFE, in square inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Given the true statement: The picnic on Sunday will not be held only if the weather is not fair. We can then conclude that:
Answer Choices:
A. If the picnic is held, Sunday's weather is undoubtedly fair.
B. If the picnic is not held, Sunday's weather is possibly unfair.
C. If it is not fair Sunday, the pienic will not be held.
D. If it is fair Sunday, the pienic may be held.
E. If it is fair Sunday, the picnic must be held.
Solution:
Problem 18: If is used as an approximation to the value of , the ratio of the error made to the correct value is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: If is exactly divisible by , the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: For every the sum of terms of an arithmetic progression is . The term is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: It is possible to choose in such a way that the value of is:
Answer Choices:
A.
B.
C.
D. smaller than any positive number that might be specified
E. greater than any positive number that might be specified
Solution:
Problem 22: If and and are the roots of , then the equality holds:
Answer Choices:
A. for all values of
B. for all values of
C. only when
D. only when or
E. only when or
Solution:
Problem 23: If we write for all such that , the smallest value we can use for N is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Given the sequence , the smallest value of n such that the product of the first members of this sequence exceeds is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let ABCD be a quadrilateral with AB extended to E so that . Lines and CE are drawn to form angle ACE. For this angle to be a right angle it is necessary that quadrilateral have:
Answer Choices:
A. all angles equal
B. all sides equal
C. two pairs of equal sides
D. one pair of equal sides
E. one pair of equal angles
Solution:
Problem 26: For the numbers , e define to be the arithmetic mean of all five numbers; to be the arithmetic mean of and to be the arithmetic mean of , and ; and to be the arithmetic mean of and . Then, no matter how , e are chosen, we shall always have:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 27: When is divided by the quotient is and the remainder is . When is divided by the quotient is and the remainder is . If then is:
Answer Choices:
A.
B.
C.
D.
E. an undetermined constant
Solution:
Problem 28: An escalator (moving staircase) of uniform steps visible at all times descends at constant speed. Two boys, A and Z, walk down the escalator steadily as it moves, A negotiating twice as many escalator steps per minute as Z . A reaches the bottom after taking 27 steps while Z reaches the bottom after taking 18 steps. Then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Of 28 students taking at least one subject the number taking Mathematics and English only equals the number taking Mathematics only. No student takes English only or History only, and six students take Mathematics and History, but no English. The number taking English and History only is five times the number taking all three subjects. If the number taking all three subjects is even and non-zero, the number taking English and Mathematics only is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Let BC of right triangle ABC be the diameter of a circle intersecting hypotenuse AB in D . At D a tangent is drawn cutting leg CA in F. This information is not sufficient to prove that:
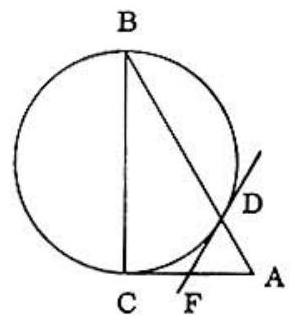
Answer Choices:
A. DF bisects CA
B. DF bisects
C.
D.
E.
Solution:
Problem 31: The number of real values of satisfying the equality , where , is:
Answer Choices:
A.
B.
C.
D. a finite integer greater than 2
E. not finite
Solution:
Problem 32: An article costing dollars is sold for at a loss of x percent of the selling price. It is then resold at a profit of percent of the new selling price . If the difference between and is dollars, then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: If the number 15 !, that is, , ends with zeros when given to the base 12 and ends with zeros when given to the base 10 , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: For the smallest value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: The length of a rectangle is 5 inches and its width is less than 4 inches. The rectangle is folded so that two diagonally opposite vertices coincide. If the length of the crease if , then the width is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: Given distinct straight lines OA and OB . From a point in OA a perpendicular is drawn to OB; from the foot of this perpendicular a line is drawn perpendicular to OA. From the foot of this second perpendicular a line is drawn perpendicular to OB; and so on indefinitely. The lengths of the first and second perpendiculars are and , respectively. Then the sum of the lengths of the perpendiculars approaches a limit as the number of perpendiculars grows beyond all bounds. This limit is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: Point is selected on side of triangle in such a way that and point D is selected on side so that . The point of intersection of AD and CE is F . Then is:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: A takes m times as long to do a piece of work as B and C together; B takes times as long as and together; and takes times as long as and together. Then x , in terms of m and n , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 39: A foreman noticed an inspector checking a -hole with a -plug and a -plug and suggested that two more gauges be inserted to be sure that the fit was snug. If the new gauges are alike, then the diameter, , of each, to the nearest hundredth of an inch, is:
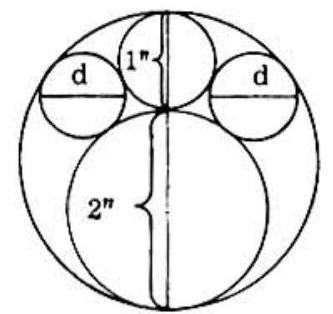
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: Let be the number of integer values of such that is the square of an integer. Then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions