¶ 1966 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1966 AHSME problems, please refer below:
Problem 1: Given that the ratio of to is constant, and when , then, when equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: When the base of a triangle is increased and the altitude to this base is decreased , the change in area is:
Answer Choices:
A. increase
B. increase
C.
D. decrease
E. decrease
Solution:
Problem 3: If the arithmetic mean of two numbers is 6 and their geometric mean is 10 , then an equation with the given two numbers as roots is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Circle I is circumscribed about a given square and circle II is inscribed in the given square. If is the ratio of the area of circle I to that of circle II, then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The number of values of satisfying the equation is:
Answer Choices:
A.
B.
C.
D.
E. an integer greater than 3
Solution:
Problem 6: AB is a diameter of a circle centered at is a point on the circle such that angle BOC is . If the diameter of the circle is 5 inches, the length of chord AC, expressed in inches, is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 7: Let be an identity in . The numerical value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The length of the common chord of two intersecting circles is 16 feet. If the radii are 10 feet and 17 feet, the distance between the centers of the circles, expressed in feet, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If the sum of two numbers is 1 and their product is 1 , then the sum of their cubes is ( ):
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The sides of triangle BAC are in the ratio . BD is the angle-bisector drawn to the shortest side , dividing it into segments and . If the length of is 10 , then the length of the longer segment of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The number of real values of that satisfy the equation is:
Answer Choices:
A.
B.
C.
D.
E. greater than 3
Solution:
Problem 13: The number of points with positive rational coordinates selected from the set of points in the -plane such that , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The length of rectangle is 5 inches and its width is 3 inches. Diagonal is divided into three equal segments by points and . The area of triangle BEF, expressed in square inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If and , then:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If and and real numbers, then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The number of distinct points common to the curves and is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In a given arithmetic sequence the first term is 2 , the last term is 29 , and the sum of all the terms is 155 . The common difference is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let be the sum of the first terms of the arithmetic sequence and let be the sum of the first terms of the arithmetic sequence . Then for:
Answer Choices:
A. no value of
B. one value of
C. two values of
D. four values of
E. a value of n greater than four
Solution:
Problem 20: The negation of the proposition "For real values of and , if , then " is:
Answer Choices:
A. If , then
B. If , then
C. If , then
D. If , then
E. If , then
Solution:
Problem 21: An '-pointed star' is formed as follows: the sides of a convex polygon are numbered consecutively ; for all values of , sides and are non-parallel, sides and being respectively identical with sides 1 and 2; prolong the pairs of sides numbered and until they meet.
(A figure is shown for the case ).
Let be the degree-sum of the interior angles at the points of the star; then equals:
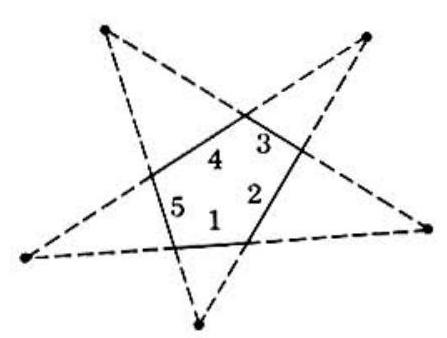
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Consider the statements: (I) (II) (III) (IV) , where we allow and to be real or complex numbers. Those statements for which there exist solutions other than and , are:
Answer Choices:
A. (I), (II), (III), (IV)
B. (II), (III), (IV) only
C. (I), (III), (IV) only
D. (III), (IV) only
E. (I) only
Solution:
Problem 23: If is real and , then the complete set of values of for which is real, is:
Answer Choices:
A. and
B. and
C. and
D.
E.
Solution:
Problem 24: If , then equals:
Answer Choices:
A.
B.
C.
D.
E. a number greater than 2 and less than 10
Solution:
Problem 25: If and , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Let be a positive integer and let the lines and intersect in a point whose coordinates are integers. Then can be:
Answer Choices:
A. 4 only
B. 5 only
C. 6 only
D. 7 only
E. one of the integers and one other positive integer
Solution:
Problem 27: At his usual rate a man rows 15 miles downstream in five hours less time than it takes him to return. If he doubles his usual rate, the time downstream is only one hour less than the time upstream. In miles per hour, the rate of the stream's current is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Five points are taken in order on a straight line with distances , and . is a point on the line between B and and such that . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: The number of positive integers less than 1000 divisible by neither 5 nor 7, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: If three of the roots of are 1,2, and 3, then the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: Triangle is inscribed in a circle with center . A circle with center O is inscribed in triangle . is drawn, and extended to intersect the larger circle in . Then we must have:
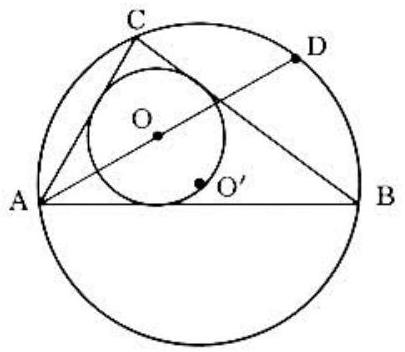
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: Let be the midpoint of side of triangle . Let be a point in between and , and let be drawn parallel to and intersecting at . If the ratio of the area of triangle to that of triangle is designated by , then
Answer Choices:
A. depending upon the position of
B. independent of the position of
C. depending upon the position of
D. depending upon the position of
E. independent of the position of
Solution:
Problem 33: If and the number of distinct values of satisfying the equa, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: Let be the speed in miles per hour at which a wheel, 11 feet in circumference, travels. If the time for a complete rotation of the wheel is shortened by of a second, the speed is increased by 5 miles per hour. Then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: Let be an interior point of triangle and let . If , then
Answer Choices:
A. for every triangle
B. for every triangle
C. for every triangle
D. for every triangle
E. (E) neither (A) nor (B) nor (C) nor (D) applies to every triangle
Solution:
Problem 36: Let be an identity in . If we let , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: Three men, Alpha, Beta, and Gamma, working together, do a job in 6 hours less time than Alpha alone, in 1 hour less time than Beta alone, and in one-half the time needed by Gamma when working alone. Let be the number of hours needed by Alpha and Beta, working together, to do the job. Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: In triangle the medians and to sides and , respectively intersect in point . is the midpoint of side and MP intersects in . If the area of triangle is , then the area of triangle is:
Answer Choices:
A. 16 n
B. 18 n
C. 21 n
D. 24 n
E. 27 n
Solution:
Problem 39: In base the expanded fraction becomes and the expanded fraction becomes . In base fraction , when expanded, becomes while fraction becomes . The sum of and , each written in the base ten, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: In this figure AB is a diameter of a circle, centered at O, with radius a. A chord AD is drawn and extended to meet the tangent to the circle at B, in point C. Point E is taken on AC so that . If the coordinates of E are ( ), then:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions