¶ 1967 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1967 AHSME problems, please refer below:
Problem 1: The three-digit number is added to the number to give the three-digit number . If is divisible by , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: An equivalent of the expression , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The side of an equilateral triangle is . A circle is inscribed in the triangle and a square is inscribed in the circle. The area of the square is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Given , all logarithms to the same base and . If , then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A triangle is circumscribed about a circle of radius inches. If the perimeter of the triangle is inches and the area is square inches, then is:
Answer Choices:
A. independent of the value of
B.
C.
D.
E.
Solution:
Problem 6: If then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If where are real numbers and , then:
Answer Choices:
A. a must be negative
B. a must be positive
C. a must not be zero
D. a can be negative or zero, but not positive
E. a can be positive, negative, or zero
Solution:
Problem 8: To m ounces of an solution of acid, x ounces of water are added to yield an solution. If , then is:
Answer Choices:
A.
B.
C.
D.
E. not determined by the given information
Solution:
Problem 9: Let K , in square units, be the area of a trapezoid such that the shorter base, the altitude, and the longer base, in that order, are in arithmetic progression. Then:
Answer Choices:
A. K must be an integer.
B. K must be a rational fraction
C. K must be an irrational number
D. K must be an integer or a rational fraction
E. taken alone neither (A) nor (B) nor (C) nor (D) is true
Solution:
Problem 10: If is an identity for positive rational values of , then the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: If the perimeter of rectangle is 20 inches, the least value of diagonal , in inches, is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 12: If the (convex) area bounded by the -axis and the lines , and is 7 , then equals:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 13: A triangle is to be constructed given side a (opposite angle ), angle , and , the altitude from . If is the number of noncongruent solutions, then N
Answer Choices:
A. is
B. is
C. must be zero
D. must be infinite
E. must be zero or infinite
Solution:
Problem 14: Let . If , then can be expressed as:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The difference in the areas of two similar triangles is 18 square feet, and the ratio of the larger area to the smaller is the square of an integer. The area of the smaller triangle, in square feet, is an integer, and one of its sides is 3 feet. The corresponding side of the larger triangle, in feet, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let the product (12)(15)(16), each factor written in base b, equal 3146 in base b. Let , each term expressed in base . Then , in base , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If and are the distinct real roots of ; then it must follow that:
Answer Choices:
A.
B. or
C. and
D. and
E.
Solution:
Problem 18: If and then
Answer Choices:
A. P can take any real value
B. P
C. P
D.
E.
Solution:
Problem 19: The area of a rectangle remains unchanged when it is made inches longer and inch narrower, or when it is made inches shorter and inch wider. Its area, in square inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A circle is inscribed in a square of side , then a square is inscribed in that circle, then a circle is inscribed in the latter square, and so on. If is the sum of the areas of the first n circles so inscribed, then, as n grows beyond all bounds, approaches:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: In right triangle the hypotenuse and leg . The bisector of angle meets the opposite side in . A second right triangle is then constructed with hypotenuse and leg . If the bisector of angle meets the opposite side in , the length of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: For the natural numbers, when is divided by D , the quotient is and the remainder is . When is divided by , the quotient is and the remainder is . Then, when is divided by , the remainder is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If is real and positive and grows beyond all bounds, then approaches:
Answer Choices:
A.
B.
C.
D.
E. no finite number
Solution:
Problem 24: The number of solution-pairs in positive integers of the equation is:
Answer Choices:
A.
B.
C.
D.
E. none of these.
Solution:
Problem 25: For every odd number we have:
Answer Choices:
A. is divisible by
B. is divisible by
C. is divisible by
D. is divisible by
E. is divisible by
Solution:
Problem 26: If one uses only the tabular information , , then the strongest statement one can make for is that it lies between:
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 27: Two candles of the same length are made of different materials so that one burns out completely at a uniform rate in 3 hours and the other, in 4 hours. At what time P.M. should the candles be lighted so that, at 4 P.M., one stub is twice the length of the other?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Given the two hypotheses: I Some Mems are not Ens and II No Ens are Vees. If "some" means "at least one", we can conclude that:
Answer Choices:
A. Some Mems are not Vees
B. Some Vees are not Mems
C. No Mem is a Vee
D. Some Mems are Vees
E. Neither (A) nor (B) nor (C) nor (D) is deducible from the given statements.
Solution:
Problem 29: is a diameter of a circle. Tangents and are drawn so that and BD intersect in a point on the circle. If and , the diameter of the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: A dealer bought n radios for d dollars, d , a positive integer. He contributed two radios to a community bazaar at half their cost. The rest he sold at a profit of on each radio sold. If the overall profit was , then the least possible value of n for the given information is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: Let where are consecutive integers and . Then is:
Answer Choices:
A. always an even integer
B. sometimes an odd integer, sometimes not
C. always an odd integer
D. sometimes rational, sometimes not
E. always irrational
Solution:
Problem 32: In quadrilateral ABCD with diagonals AC and BD , intersecting at , , and . The length of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: In this diagram semi-circles are constructed on diameters , and , so that they are mutually tangent. If , then the ratio of the shaded area to the area of a circle with as radius is:
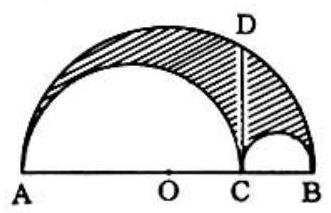
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: Points are taken respectively on sides , and of triangle ABC so that . The ratio of the area of triangle to that of triangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: The roots of are in arithmetic progression. The difference between the largest and smallest roots is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: Given a geometric progression of five terms, each a positive integer less than 100. The sum of the five terms is 211 . If is the sum of those terms in the progression which are squares of integers, then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: Segments are drawn from the vertices of triangle , each perpendicular to a straight line , not intersecting the triangle. Points D,E,F are the intersection points of RS with the perpendiculars. If is the length of the perpendicular segment drawn to from the intersection point of the medians of the triangle, then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: Given a set consisting of two undefined elements "pib" and "maa", and the four postulates: : Every pib is a collection of maas, : Any two distinct pibs have one and only one maa in common, : Every maa belongs to two and only two pibs, : There are exactly four pibs.
Consider the three theorems: : There are exactly six maas, : There are exactly three maas in each pib, : For each maa there is exactly one other maa not in the same pib with it. The theorems which are deducible from the postulates are:
Answer Choices:
A. only
B. and only
C. and only
D. and only
E.
Solution:
Problem 39: Given the sets of consecutive integers , where each set contains one more element than the preceding one, and where the first element of each succeeding set is one more than the last element of the preceding set. Let be the sum of the elements in the nth set. Then equals:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 40: Located inside equilateral triangle is point such that , and . To the nearest integer the area of triangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions