¶ 2025 AMC12A Problems and Solutions
Problem 1: Andy and Betsy both live in Mathville. Andy leaves Mathville on his bicycle at , traveling due north at a steady miles per hour. Betsy leaves on her bicycle from the same point at , traveling due east at a steady miles per hour. At what time will they be exactly the same distance from their common starting point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A box contains pounds of a nut mix that is percent peanuts, percent cashews, and percent almonds. A second nut mix containing percent peanuts, percent cashews, and percent almonds is added to the box resulting in a new nut mix that is percent peanuts. How many pounds of cashews are now in the box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A team of students is going to compete against a team of teachers in a trivia contest. The total number of students and teachers is . Ash, a cousin of one of the students, wants to join the contest. If Ash plays with the students, the average age on that team will increase from to . If Ash plays with the teachers, the average age on that team will decrease from to . How old is Ash?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Agnes writes the following four statements on a blank piece of paper.
- At least one of these statements is true.
- At least two of these statements are true.
- At least two of these statements are false.
- At least one of these statements is false.
Each statement is either true or false. How many false statements did Agnes write on the paper?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In the figure below, the outside square contains infinitely many squares, each of them with the same center and sides parallel to the outside square. The ratio of the side length of a square to the side length of the next inner square is , where . The spaces between squares are alternately shaded, as shown in the figure (which is not necessarily drawn to scale).

The area of the shaded portion of the figure is of the area of the original square. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Six chairs are arranged around a round table. Two students and two teachers randomly select four of the chairs to sit in. What is the probability that the two students will sit in two adjacent chairs and the two teachers will also sit in two adjacent chairs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In a certain alien world, the maximum running speed of an organism is dependent on its number of toes and number of eyes . The relationship can be expressed as centimeters per hour, where are integer constants. In a population where all organisms have toes, ; and in a population where all organisms have eyes, (base ). What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Pentagon is inscribed in a circle, and . Let and intersect at point , and suppose that and . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Let . What real number has the property that , , and are three collinear points in the complex plane?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In the figure shown below, major arc and minor arc have the same center . Also, lies between and , and lies between and . Major arc , minor arc , and each of the two segments and have length .
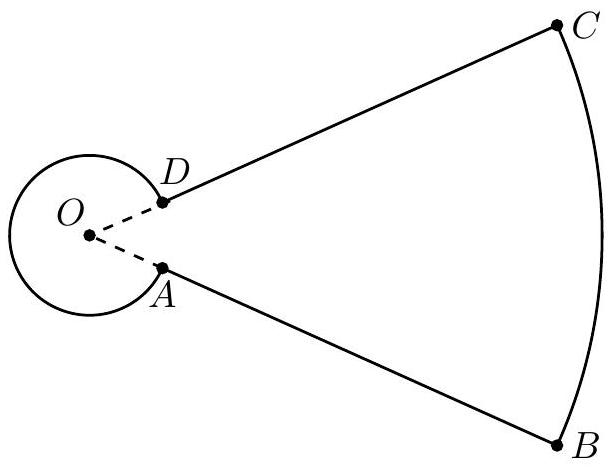
What is the distance from to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The orthocenter of a triangle is the concurrent intersection of the three (possibly extended) altitudes. What is the sum of the coordinates of the orthocenter of the triangle whose vertices are , , and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The harmonic mean of a collection of numbers is the reciprocal of the arithmetic mean of the reciprocals of the numbers in the collection. For example, the harmonic mean of is
What is the harmonic mean of all the real roots of the degree polynomial
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Let . Let be the greatest integer such that there exists a subset of with elements that does not contain five consecutive integers. Suppose integers are chosen at random from without replacement. What is the probability that the chosen elements do not include five consecutive integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Points and are collinear with between and . The ellipse with foci at and is internally tangent to the ellipse with foci at and , as shown below.
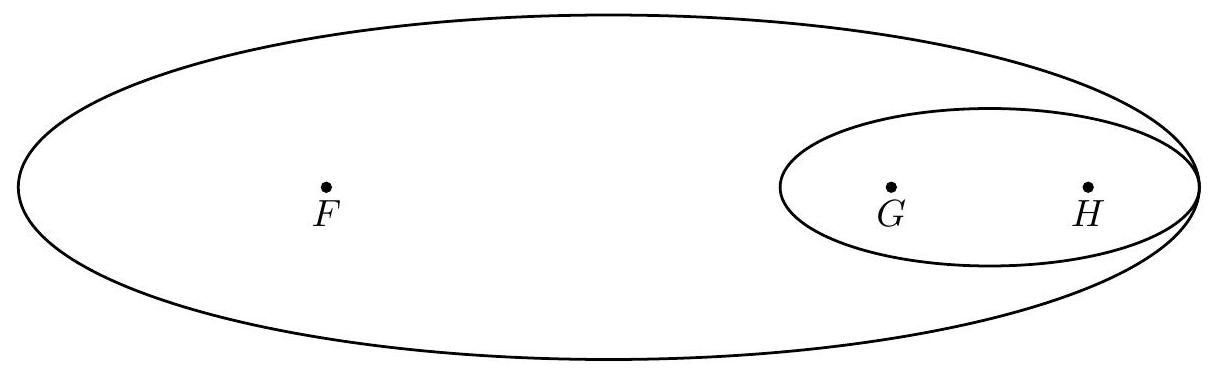
The two ellipses have the same eccentricity , and the ratio of their areas is . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A set of numbers is called sum-free if whenever and are (not necessarily distinct) elements of the set, is not an element of the set. For example, and the empty set are sum-free, but is not. What is the greatest possible number of elements in a sum-free subset of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Triangle has side lengths , , and . The bisector of and the altitude to side intersect at point . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The polynomial has three roots in the complex plane. What is the area of the triangle formed by these roots?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: How many ordered triples of distinct nonnegative integers satisfy and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let be the roots of . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The base of the pentahedron shown below is a rectangle, and its lateral faces are two isosceles triangles with base and congruent sides , and two isosceles trapezoids with bases and and nonparallel sides .
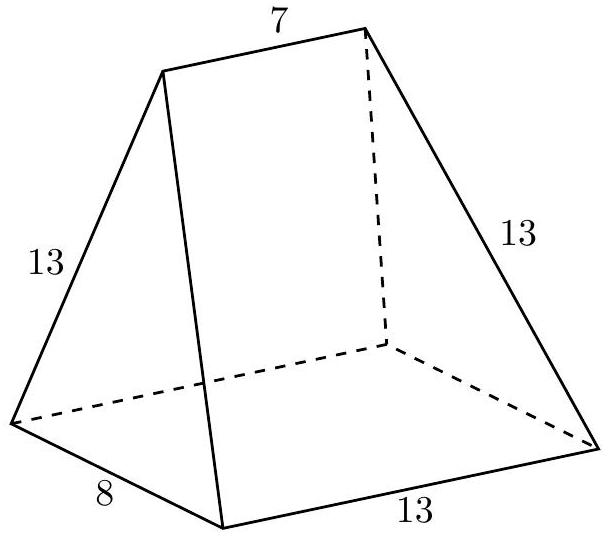
What is the volume of the pentahedron?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: There is a unique ordered triple of nonnegative integers such that
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Three real numbers are chosen independently and uniformly at random between and . What is the probability that the greatest of these three numbers is greater than times each of the other two numbers? (If the chosen numbers are , then .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Call a positive integer fair if no digit is used more than once, it has no s, and no digit is adjacent to two greater digits. For example, , and are fair, but , and are not fair. How many fair positive integers are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A circle of radius is surrounded by circles of radius , externally tangent to the central circle and sequentially tangent to each other, as shown. Then can be written as , where are integers. What is
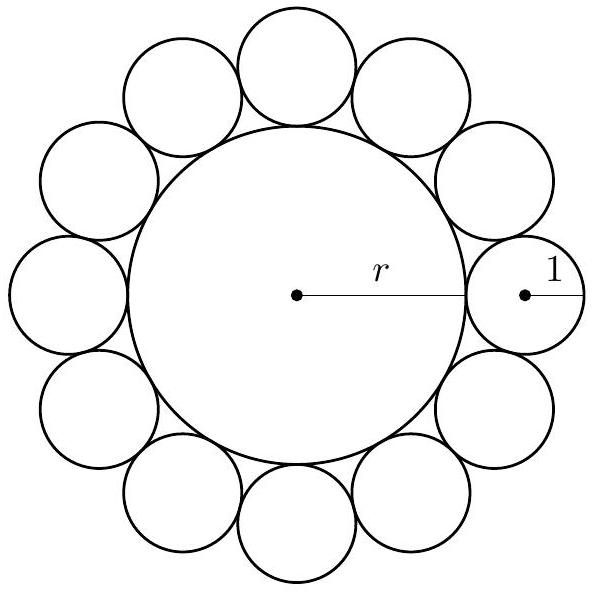
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Polynomials and each have degree and leading coefficient , and their roots are all elements of . The function has the property that there exist real numbers such that the set of all real numbers with consists of the closed interval together with the open interval . How many functions are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions