¶ 1954 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1954 AHSME problems, please refer below:
Problem 1: The square of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The equation can be transformed by eliminating fractions to the equation . The roots of the latter equation are 4 and 1 . Then the roots of the first equation are:
Answer Choices:
A. and
B. only
C. only
D. neither nor
E. and some other root
Solution:
Problem 3: If varies as the cube of , and varies as the fifth root of , then varies as the th power of , where is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If the Highest Common Divisor of 6432 and 132 is diminished by 8, it will equal:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A regular hexagon is inscribed in a circle of radius 10 inches. Its area is:
Answer Choices:
A. sq. in.
B. sq . in.
C. sq. in.
D. sq. in.
E. sq. in.
Solution:
Problem 6: The value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A housewife saved in buying a dress on sale. If she spent for the dress, she saved about:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The base of a triangle is twice as long as a side of a square and their areas are the same. Then the ratio of the altitude of the triangle to the side of the square is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A point is outside a circle and is 13 inches from the center. A secant from cuts the circle at and so that the external segment of the secant is 9 inches and is 7 inches. The radius of the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The sum of the numerical coefficients in the expansion of the binomial is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A merchant placed on display some dresses, each with a marked price. He then posted a sign " off on these dresses." The cost of the dresses was of the price at which he actually sold them. Then the ratio of the cost to the marked price was:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The solution of the equations is:
Answer Choices:
A.
B.
C. There is no solution
D. There is an unlimited number of solutions
E.
Solution:
Problem 13: A quadrilateral is inscribed in a circle. If angles are inscribed in the four arcs cut off by the sides of the quadrilateral, their sum will be:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: When simplified equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The graph of the function goes:
Answer Choices:
A. up to the right and down to the left
B. down to the right and up to the left
C. up to the right and up to the left
D. down to the right and down to the left
E. none of these ways
Solution:
Problem 18: Of the following sets, the one that includes all values of which will satisfy is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: If the three points of contact of a circle inscribed in a triangle are joined, the angles of the resulting triangle:
Answer Choices:
A. are always equal to
B. are always one obtuse angle and two unequal acute angles
C. are always one obtuse angle and two equal acute angles
D. are always acute angles
E. are always unequal to each other
Solution:
Problem 20: The equation has:
Answer Choices:
A. no negative real roots
B. no positive real roots
C. no real roots
D. positive and negative roots
E. positive and negative root
Solution:
Problem 21: The roots of the equation can be found by solving:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The expression cannot be evaluated for or , since division by zero is not allowed. For other values of :
Answer Choices:
A. The expression takes on many different values.
B. The expression has only the value .
C. The expression has only the value .
D. The expression always has a value between and .
E. The expression has a value greater than or less than .
Solution:
Problem 23: If the margin made on an article costing dollars and selling for dollars is , then the margin is given by:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The values of for which the equation will have real and equal roots are:
Answer Choices:
A. and
B. only
C. and
D. and
E. only
Solution:
Problem 25: The two roots of the equation are 1 and:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: The straight line is divided at so that . Circles are described on and as diameters and a common tangent meets produced at . Then equals:
Answer Choices:
A. diameter of the smaller circle
B. radius of the smaller circle
C. radius of the larger circle
D.
E. the difference of the two radii.
Solution:
Problem 27: A right circular cone has for its base a circle having the same radius as a given sphere. The volume of the cone is one-half that of the sphere. The ratio of the altitude of the cone to the radius of its base is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: If and , the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: If the ratio of the legs of a right triangle is , then the ratio of the corresponding segments of the hypotenuse made by a perpendicular upon it from the vertex is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: and together can do a job in 2 days; and can do it in four days; and and in days. The number of days required for to do the job alone is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: In triangle , angle . Point is within the triangle with angle angle . The number of degrees in angle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: The factors of are:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: A bank charges for a loan of . The borrower receives and repays the loan in 12 installments of a month. The interest rate is approximately:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: The fraction, :
Answer Choices:
A. equals
B. is less than by
C. is less than 0.33333333 by
D. is greater than 0.33333333 by
E. is greater than 0.33333333 by
Solution:
Problem 35: In the right triangle shown the sum of the distances and is equal to the sum of the distances and . If , and , then equals:
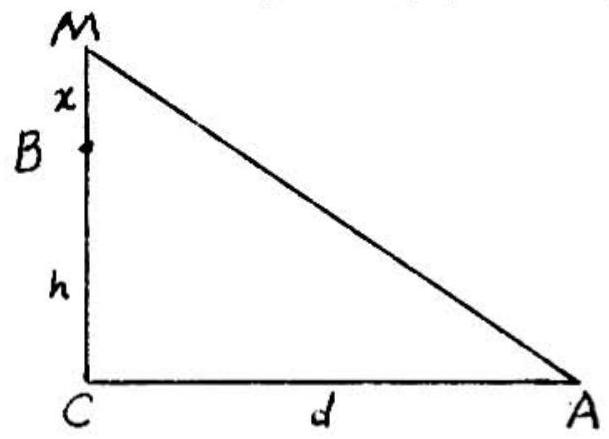
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: A boat has a speed of . in still water. In a stream that has a current of . it travels a certain distance downstream and returns. The ratio of the average speed for the round trip to the speed in still water is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: Given triangle with bisecting angle extended to and angle a right angle, then:
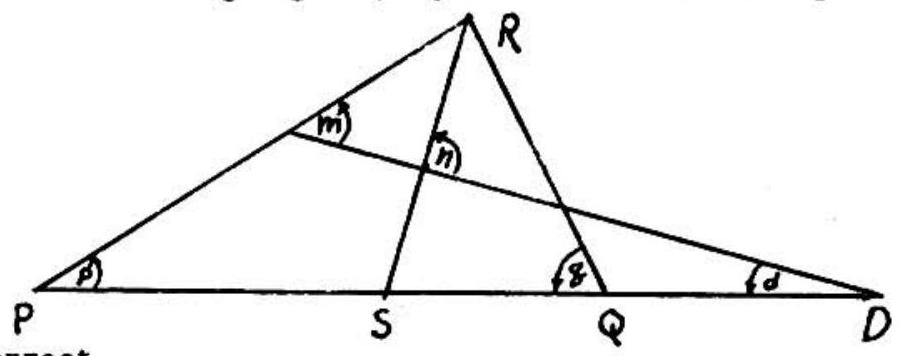
Answer Choices:
A.
B.
C.
D.
E. none of these is correct.
Solution:
Problem 38: If and , the value of when is approximately:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 39: The locus of the mid-point of a line segment that is drawn from a given external point to a given circle with center and radius , is:
Answer Choices:
A. a straight line perpendicular to
B. a straight line parallel to
C. a circle with center and radius
D. a circle with center at the midpoint of and radius
E. a circle with center at the mid-point and radius
Solution:
Problem 40: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 41: The sum of all the roots of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 42: Consider the graphs of (1) and (2) on the same set of axis. These parabolas are exactly the same shape. Then:
Answer Choices:
A. the graphs coincide.
B. the graph of (1) is lower than the graph of (2).
C. the graph of (1) is to the left of the graph of (2).
D. The graph of (1) is to the right of the graph of (2).
E. The graph of (1) is higher than the graph of (2).
Solution:
Problem 43: The hypotenuse of a right triangle is 10 inches and the radius of the inscribed circle is 1 inch. The perimeter of the triangle in inches is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 44: A man born in the first half of the nineteenth century was years old in the year . He was born in:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 45: In a rhombus, , line segments are drawn within the rhombus, parallel to diagonal , and terminated in the sides of the rhombus. A graph is drawn showing the length of a segment as a function of its distance from vertex . The graph is:
Answer Choices:
A. A straight line passing through the origin.
B. A straight line cutting across the upper right quadrant.
C. Two line segments forming an upright .
D. Two line segments forming an inverted .
E. None of these.
Solution:
Problem 46: In the diagram if points are points of tangency, then equals:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 47: At the midpoint of line segment which is units long, a perpendicular is erected with length units. An arc is described from with a radius equal to , meeting at . Then and are the roots of:
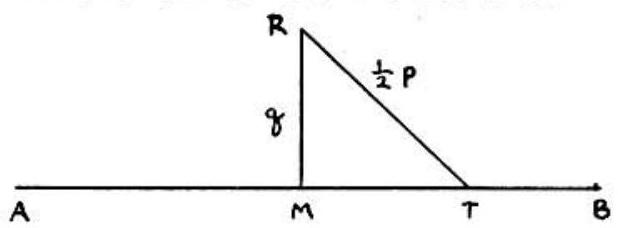
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 48: A train, an hour after starting, meets with an accident which detains it a half hour, after which it proceeds at of its former rate and arrives hours late. Had the accident happened miles farther along the line, it would have arrived only hours late. The length of the trip in miles was:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 49: The difference of the squares of two odd numbers is always divisible by 8. If , and and are the odd numbers, to prove the given statement we put the difference of the squares in the form:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 50: The times between and o clock, correct to the nearest minute, when the hands of a clock will form an angle of degrees are:
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions