¶ 1999 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1999 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Which one of the following statements is false?
Answer Choices:
A. All equilateral triangles are congruent to each other.
B. All equilateral triangles are convex.
C. All equilateral triangles are equiangular.
D. All equilateral triangles are regular polygons.
E. All equilateral triangles are similar to each other.
Solution:
Problem 3: The number halfway between and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Find the sum of all prime numbers between and that are simultaneously greater than a multiple of and less than a multiple of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The marked price of a book was less than the suggested retail price. Alice purchased the book for half the marked price at a Fiftieth Anniversary sale. What percent of the suggested retail price did Alice pay?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: What is the sum of the digits of the decimal form of the product
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the largest number of acute angles that a convex hexagon can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: At the end of Walter was half as old as his grandmother. The sum of the years in which they were born is . How old will Walter be at the end of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Before Ashley started a three-hour drive, her car's odometer reading was , a palindrome. (A palindrome is a number that reads the same way from left to right as it does from right to left.) At her destination, the odometer reading was another palindrome. If Ashley never exceeded the speed limit of miles per hour, which of the following was her greatest possible average speed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A sealed envelope contains a card with a single digit on it. Three of the following statements are true, and the other is false.
I. The digit is .
II. The digit is not .
III. The digit is .
IV. The digit is not .
Which one of the following must necessarily be correct?
Answer Choices:
A. I is true.
B. I is false.
C. II is true.
D. III is true.
E. IV is false.
Solution:
Problem 11: The student lockers at Olympic High are numbered consecutively beginning with locker number . The plastic digits used to number the lockers cost two cents apiece. Thus, it costs two cents to label locker number and four cents to label locker number . If it costs to label all the lockers, how many lockers are there at the school?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: What is the maximum number of points of intersection of the graphs of two different fourth degree polynomial functions and , each with leading coefficient
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Define a sequence of real numbers by and for all . Then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 14: Four girls - Mary, Alina, Tina, and Hanna - sang songs in a concert as trios, with one girl sitting out each time. Hanna sang songs, which was more than any other girl, and Mary sang songs, which was fewer than any other girl. How many songs did these trios sing?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let be a real number such that . Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: What is the radius of a circle inscribed in a rhombus with diagonals of length and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be a polynomial such that when is divided by , the remainder is , and when is divided by , the remainder is . What is the remainder when is divided by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: How many zeros does have on the interval
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 19: Consider all triangles satisfying the following conditions: is a point on for which and are integers, and . Among all such triangles, the smallest possible value of is
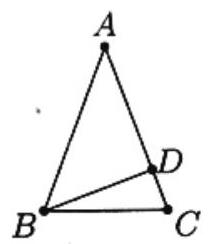
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The sequence satisfies , and, for all is the arithmetic mean of the first terms. Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A circle is circumscribed about a triangle with sides , and , thus dividing the interior of the circle into four regions. Let , and be the areas of the non-triangular regions, with being the largest. Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The graphs of and intersect at points and . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The equiangular convex hexagon has , and . The area of the hexagon is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Six points on a circle are given. Four of the chords joining pairs of the six points are selected at random. What is the probability that the four chords form a convex quadrilateral?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: There are unique integers such that
where for . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Three non-overlapping regular plane polygons, at least two of which are congruent, all have sides of length . The polygons meet at a point in such a way that the sum of the three interior angles at is . Thus the three polygons form a new polygon with as an interior point. What is the largest possible perimeter that this polygon can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: In triangle and . Then in degrees is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Let be a sequence of integers such that
, for ;
; and
.
Let and be the minimal and maximal possible values of , respectively. Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: A tetrahedron with four equilateral triangular faces has a sphere inscribed within it and a sphere circumscribed about it. For each of the four faces, there is a sphere tangent externally to the face at its center and to the circumscribed sphere. A point is selected at random inside the circumscribed sphere. The probability that lies inside one of the five small spheres is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: The number of ordered pairs of integers for which and
is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions