¶ 2022 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2022 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2022 AMC 12A math contest by visiting Random Math AMC 12A 2022 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2022 AMC 12A problems, please refer below:
Problem 1: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The sum of three numbers is . The first number is times the third number, and the third number is less than the second number. What is the absolute value of the difference between the first and second numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Five rectangles, , and , are arranged in a square as shown below. These rectangles have dimensions , and , respectively. (The figure is not drawn to scale.) Which of the five rectangles is the shaded one in the middle?
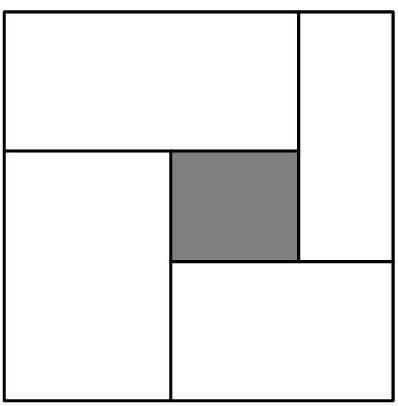
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The least common multiple of a positive integer and is , and the greatest common divisor of and is . What is the sum of the digits of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The taxicab distance between points and in the coordinate plane is given by
For how many points with integer coordinates is the taxicab distance between and the origin less than or equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A data set consists of (not distinct) positive integers: , and . The average (arithmetic mean) of the numbers equals a value in the data set. What is the sum of all possible values of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A rectangle is partitioned into regions as shown. Each region is to be painted a solid color - red, orange, yellow, blue, or green - so that regions that touch are painted different colors, and colors can be used more than once. How many different colorings are possible?
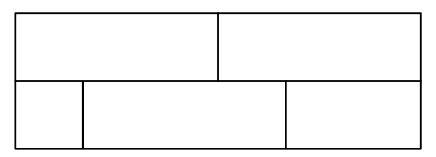
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The infinite product
evaluates to a real number. What is that number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: On Halloween children walked into the principal's office asking for candy. They can be classified into three types: Some always lie; some always tell the truth; and some alternately lie and tell the truth. The alternaters arbitrarily choose their first response, either a lie or the truth, but each subsequent statement has the opposite truth value from its predecessor. The principal asked everyone the same three questions in this order.
"Are you a truth-teller?" The principal gave a piece of candy to each of the children who answered yes.
"Are you an alternater?" The principal gave a piece of candy to each of the children who answered yes.
"Are you a liar?" The principal gave a piece of candy to each of the children who answered yes.
How many pieces of candy in all did the principal give to the children who always tell the truth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many ways are there to split the integers through into pairs such that in each pair, the greater number is at least times the lesser number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: What is the product of all real numbers such that the distance on the number line between and is twice the distance on the number line between and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be the midpoint of in regular tetrahedron . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Let be the region in the complex plane consisting of all complex numbers that can be written as the sum of complex numbers and , where lies on the segment with endpoints and , and has magnitude at most . What integer is closest to the area of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: What is the value of
where log denotes the base-ten logarithm?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The roots of the polynomial are the height, length, and width of a rectangular box (right rectangular prism). A new rectangular box is formed by lengthening each edge of the original box by units. What is the volume of the new box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A triangular number is a positive integer that can be expressed in the form , for some positive integer . The three smallest triangular numbers that are also perfect squares are , and . What is the sum of the digits of the fourth smallest triangular number that is also a perfect square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Suppose is a real number such that the equation
has more than one solution in the interval . The set of all such that can be written in the form , where , and are real numbers with . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be the transformation of the coordinate plane that first rotates the plane degrees counterclockwise around the origin and then reflects the plane across the -axis. What is the least positive integer such that performing the sequence of transformations returns the point back to itself?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Suppose that cards numbered are arranged in a row. The task is to pick them up in numerically increasing order, working repeatedly from left to right. In the example below, cards are picked up on the first pass, and on the second pass, on the third pass, on the fourth pass, and on the fifth pass. For how many of the possible orderings of the cards will the cards be picked up in exactly two passes?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Isosceles trapezoid has parallel sides and , with and . There is a point in the plane such that , and . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let
Which of the following polynomials is a factor of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be a real number, and let and be the two complex numbers satisfying the equation . Points , and are the vertices of (convex) quadrilateral in the complex plane. When the area of obtains its maximum possible value, is closest to which of the following?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let and be the unique relatively prime positive integers such that
Let denote the least common multiple of the numbers . For how many integers with is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: How many strings of length formed from the digits are there such that for each , at least of the digits are less than ? (For example, satisfies this condition because it contains at least digit less than , at least digits less than , at least digits less than , and at least digits less than . The string does not satisfy the condition because it does not contain at least digits less than .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A circle with integer radius is centered at . Distinct line segments of length connect points to for and are tangent to the circle, where , and are all positive integers and . What is the ratio for the least possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions