¶ 2021 AMC 12B Spring Problems and Solutions
Problem Set Workbook
The downloadable workbook for 2021 AMC 12B Spring problems is available here.
Discussion Forum
Engage in discussion about the 2021 AMC 12B_Spring math contest by visiting Random Math AMC 12B_Spring 2021 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2021 AMC 12B_Spring problems, please refer below:
Problem 1: How many integer values satisfy
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: At a math contest, students are wearing blue shirts, and another students are wearing yellow shirts. The students are assigned into points. In exactly of these pairs, both students are wearing blue shirts. In how many pairs are both students wearing yellow shirts?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Suppose
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Ms. Blackwell gives an exam to two classes. The mean of the scores of the students in the morning class is , and the afternoon class mean score is . The ratio of the number of students in the morning class to the number of students in the afternoon class is . What is the mean of the scores of all the students?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The point in the -plane is first rotated counterclockwise by around the point and then reflected about the line . The image of after these two transformations is at . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: An inverted cone with base radius and height is full of water. The water is poured into a tall cylinder whose horizontal base has a radius of . What is the height in centimeters of the water in the cylinder?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Let . What is the ratio of the sum of the odd divisors of to the sum of the even divisors of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Three equally spaced parallel lines intersect a circle, creating three chords of lengths , and . What is the distance between two adjacent parallel lines?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Two distinct numbers are selected from the set so that the sum of the remaining numbers is the product of these two numbers. What is the difference of these two numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Triangle has and . Let be the point on such that . There are exactly two points and on line such that quadrilaterals and are trapezoids. What is the distance
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Suppose that is a finite set of positive integers. If the greatest integer in is removed from , then the average value (arithmetic mean) of the integers remaining is . If the least integer is is also removed, then the average value of the integers remaining is . If the greatest integer is then returned to the set, the average value of the integers rises to . The greatest integer in the original set is greater than the least integer in . What is the average value of all the integers in the set
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many values of in the interval satisfy
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let be a rectangle and let be a segment perpendicular to the plane of . Suppose that has integer length, and the lengths of , and are consecutive odd positive integers (in this order). What is the volume of pyramid
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The figure below is constructed from line segments, each of which has length . The area of pentagon can be written as , where and are positive integers. What is
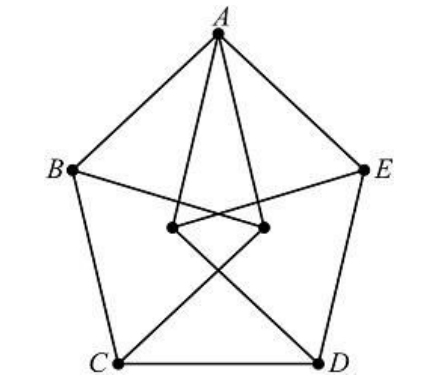
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let be a polynomial with leading coefficient , whose three roots are the reciprocals of the three roots of , where . What is in terms of , and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be an isoceles trapezoid having parallel bases and with . Line segments from a point inside to the vertices divide the trapezoid into four triangles whose areas are , and starting with the triangle with base and moving clockwise as shown in the diagram below. What is the ratio
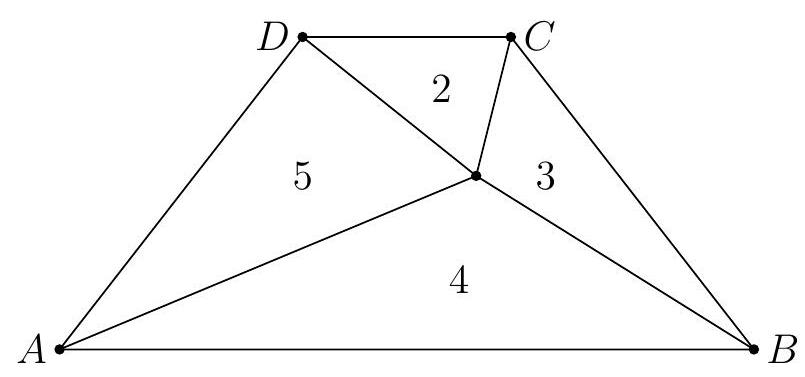
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a complex number satisfying
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Two fair dice, each with at least faces, are rolled. On each face of each die is printed a distinct integer from to the number of faces on that die, inclusive. The probability of rolling a sum of is of the probability of rolling a sum of and the probability of rolling a sum of is . What is the least possible number of faces on the two dice combined?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let and be the unique polynomials such that
and the degree of is less than . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let be the sum of all positive real numbers for which
Which of the following statements is true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Arjun and Beth play a game in which they take turns removing one brick or two adjacent bricks from one "wall" among a set of several walls of bricks, with gaps possibly creating new walls. The walls are one brick tall. For example, a set of walls of sizes and can be changed into any of the following by one move: , or . Arjun plays first, and the player who removes the last brick wins. For which starting configuration is there a strategy that guarantees a win for Beth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Three balls are randomly and independently tossed into bins numbered with the positive integers so that for each ball, the probability it is tossed into bin is for . More than one ball is allowed in each bin. The probability that the balls end up evenly spaced in distinct bins is , where and are relatively prime positive integers. (For example, the balls are evenly spaced if they are tossed into bins , and .) What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let be a parallelogram with area . Points and are the projections of and , respectively, onto the line ; and points and are the projections of and , respectively, onto the line . See the figure, which also shows the relative locations of these points.
Suppose and , and let denote the length of , the longer diagonal of . Then can be written in the form , where , and are positive integers and is not divisible by the square of any prime. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be the set of lattice points in the coordinate plane, both of whose coordinates are integers between and , inclusive. Exactly points in lie on or below a line with equation . The possible values of lie in an interval of length , where and are relatively prime positive integers. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions