¶ 2021 AMC 12A Spring Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2021 AMC 12A Spring problems here.
Discussion Forum
Engage in discussion about the 2021 AMC 12A_Spring math contest by visiting Random Math AMC 12A_Spring 2021 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2021 AMC 12A_Spring problems, please refer below:
Problem 1: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Under what conditions is true, where and are real numbers?
Answer Choices:
A. It is never true.
B. It is true if and only if .
C. It is true if and only if .
D. It is true if and only if and .
E. It is always true.
Solution:
Problem 3: The sum of two natural numbers is . One of the two numbers is divisible by . If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Tom has a collection of snakes, of which are purple and of which are happy. He observes that
- all of his happy snakes can add,
- none of his purple snakes can subtract, and
- all of his snakes that cant subtract also cant add.
Which of these conclusions can be drawn about Toms snakes?
Answer Choices:
A. Purple snakes can add.
B. Purple snakes are happy.
C. Snakes that can add are purple.
D. Happy snakes are not purple.
E. Happy snakes can't subtract.
Solution:
Problem 5: When a student multiplied the number 66 by the repeating decimal,
where and are digits, he did not notice the notation and just multiplied times . Later he found that his answer is less than the correct answer. What is the -digit integer
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A deck of cards has only red cards and black cards. The probability of a randomly chosen card being red is . When black cards are added to the deck, the probability of choosing red becomes . How many cards were in the deck originally.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the least possible value of for real numbers and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A sequence of numbers is defined by and for . What are the parities (evenness or oddness) of the triple of numbers , where denotes even and denotes odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Which of the following is equivalent to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the tops of the liquid surfaces are and . Into each cone is dropped a spherical marble of radius , which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the rise of the liquid level in the wide cone?
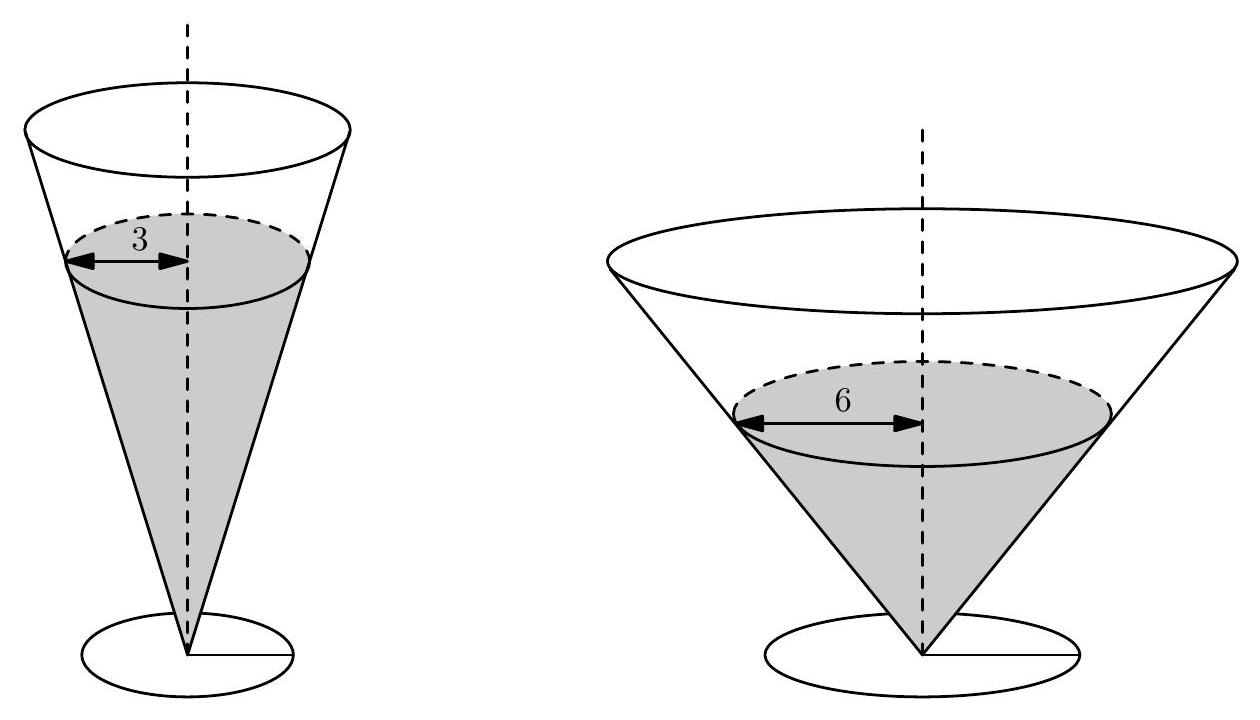
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A laser is placed at the point . The laser bean travels in a straight line. Larry wants the beam to hit and bounce off the -axis, then hit and bounce off the -axis, then hit the point . What is the total distance the beam will travel along this path?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: All the roots of polynomial are positive integers. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Of the following complex numbers , which one has the property that has the greatest real part?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A choir director must select a group of singers from among his tenors and basses. The only requirements are that the difference between the number of tenors and basses must be a multiple of , and the group must have at least one singer. Let be the number of groups that can be selected. What is the remainder when is divided by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In the following list of numbers, the integer appears times in the list for .
What is the median of the numbers in this list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Trapezoid has , and . Let be the intersection of the diagonals and , and let be the midpoint of . Glven that , the length can be written in the form , where and are positive integers and is not divisible by the square of any prime. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a function defined on the set of positive rational numbers with the property that . for all positive rational numbers and . Suppose that also has the property that for every prime number . For which of the following numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: How many solutions does the equation have in the closed interval
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose that on a parabola with vertex and a focus there exists a point such that and . What is the sum of all possible values of the length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The five solutions to the equation
may be written in the form for , where and are real. Let be the unique ellipse that passes through the points , and . The eccentricity of can be written in the form where and are relatively prime positive integers. What is (Recall that the eccentricity of an ellipse is the ratio , where is the length of the major axis of and is the is the distence between its two foci.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Suppose that the roots of the polynomial are , and , where angles are in radians. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Frieda the frog begins a sequence of hops on a grid of squares, moving one square on each hop and choosing at random the direction of each hop up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example if Frieda begins in the center square and makes two hops "up", the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Semicircle has diameter of length 14. Circle lies tangent to at a point and intersects at points and . If and , then the area of is , where and are relatively prime positive integers, and is a positive integer not divisible by the square of any prime. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let denote the number of positive integers that divide , including and . For example, , and . (This function is known as the divisor function.) Let
There is a unique positive integer such that for all positive integers . What is the sum of the digits of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions