¶ 1963 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1963 AHSME problems, please refer below:
Problem 1: Which one of the following points is not on the graph of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Let . Find n when and .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If the reciprocal of is , then equals:
Answer Choices:
A.
B.
C.
D. +1 or -1
E. none of these
Solution:
Problem 4: For what value(s) of does the pair of equations and have two identical solutions?
Answer Choices:
A.
B.
C.
D.
E. or
Solution:
Problem 5: If and are real numbers and , then:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Triangle is right-angled at . On there is a point for which and . The magnitude of angle , in degrees, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Given the four equations: (1) , (2) , (3) , (4) . The pair representing perpendicular lines is:
Answer Choices:
A. (1) and (4)
B. (1) and (3)
C. (1) and (2)
D. (2) and (4)
E. (2) and (3)
Solution:
Problem 8: The smallest positive integer x for which , where N is an integer, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In the expansion of the coefficient of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Point is taken interior to a square of side-length a and such that it is equally distant from two consecutive vertices and from the side opposite these vertices. If d represents the common distance, then d equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The arithmetic mean of a set of 50 numbers is 38 . If two numbers of the set, namely 45 and 55 , are discarded, the arithmetic mean of the remaining set of numbers is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Three vertices of parallelogram are with and diagonally opposite. The sum of the coordinates of vertex is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If , the number of integers which can possibly be negative, is, at most:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Given the equations and . If, when the roots of the equations are suitably listed, each root of the second-equation is 5 more than the corresponding root of the first equation, then equals:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 15: A circle is inscribed in an equilateral triangle, and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Three numbers , none zero, form an arithmetic progression. Increasing a by 1 or increasing c by 2 results in a geometric progression. Then b equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The expression , a real, , has the value -1 for:
Answer Choices:
A. all but two real values of
B. only two real values of
C. all real values of
D. only one real value of
E. no real values of
Solution:
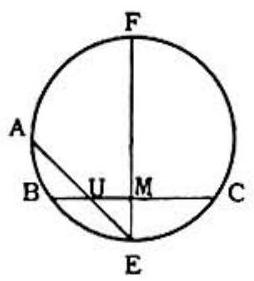
Problem 18: Chord EF is the perpendicular bisector of chord BC, intersecting it in M. Between B and M point is taken, and extended meets the circle in . Then, for any selection of , as described, triangle EUM is similar to triangle:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In counting n colored balls, some red and some black, it was found that 49 of the first 50 counted were red. Thereafter, 7 out of every 8 counted were red. If, in all, or more of the balls counted were red, the maximum value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Two men at points and miles apart, set out at the same time to walk towards each other. The man at walks uniformly at the rate of miles per hour; the man at walks at the constant rate of miles per hour for the first hour, at miles per hour for the second hour, and so on, in arithmetic progression. The men will meet miles nearer than where is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The expression has:
Answer Choices:
A. no linear factor with integer coefficients and integer exponents
B. the factor
C. the factor
D. the factor
E. the factor
Solution:
Problem 22: Acute-angled triangle is inscribed in a circle with center at , and and . A point E is taken in minor arc AC such that OE is perpendicular to AC. Then the ratio of the magnitudes of angles OBE and BAC is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A gives B as many cents as B has and C as many cents as C has. Similarly, then gives and as many cents as each then has. C, similarly, then gives A and B as many cents as each then has. If each finally has 16 cents, with how many cents does A start?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Consider equations of the form . How many such equations have real roots and have coefficients and selected from the set of integers ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
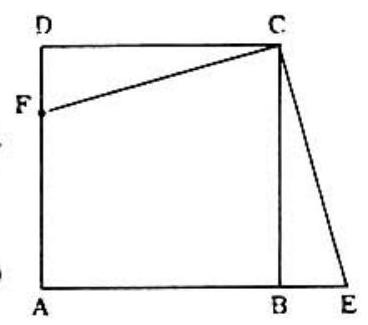
Problem 25: Point is taken in side of square . At a perpendicular is drawn to , meeting extended at . The area of is 256 square inches and the area of triangle CEF is 200 square inches. Then the number of inches in is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26:
Form I
Consider the statements (1) (3) (4) , where , and are propositions. How many of these imply the truth of ?
OR
Form II
Consider the statements (1) and are true and is false (2) is true and and are false (3) is true and and are false (4) and are true and is false. How many of these imply the truth of the statement " is implied by the statement that implies " ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Six straight lines are drawn in a plane with no two parallel and no three concurrent. The number of regions into which they divide the plane is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Given the equation with real roots. The value of for which the product of the roots of the equation is a maximum, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: A particle projected vertically upward reaches; at the end of seconds, an elevation of feet where . The highest elevation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Let . Replace each in by , and simplify. The simplified expression is equal to:
Answer Choices:
A.
B.
C. 3 F
D.
E.
Solution:
Problem 31: The number of solutions in positive integers of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: The dimensions of a rectangle are and . It is required to obtain a rectangle with dimensions and , so that its perimeter is one-third that of , and its area is one-third that of . The number of such (different) rectangles is:
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 33: Given the line and a line parallel to the given line and 4 units from it. A possible equation for is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: In triangle , side , side , and side . Let be the largest number such that the magnitude, in degrees, of the angle opposite side exceeds . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: The sides of a triangle are integers, and its area is also an integer. One side is 21 and the perimeter is 48 . The shortest side is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: A person starting with 64 cents and making 6 bets, wins three times and loses three times, the wins and losses occurring in random order. The chance for a win is equal to the chance for a loss. If each wager is for half the money remaining at the time of the bet, then the final result is:
Answer Choices:
A. a loss of
B. a gain of
C. a loss of
D. neither a gain nor a loss
E. a gain or a loss depending upon the order in which the wins and losses occur.
Solution:
Problem 37: Given seven points on a straight line, in the order stated (not necessarily evenly spaced). Let be an arbitrarily selected point on the line and let be the sum of the undirected lengths . Then s is smallest if and only if the point is:
Answer Choices:
A. midway between and
B. midway between and
C. midway between and
D. at
E. at
Solution:
Problem 38: Point F is taken on the extension of side AD of parallelogram ABCD. BF intersects diagonal AC at E and side DC at . If and , then equals:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
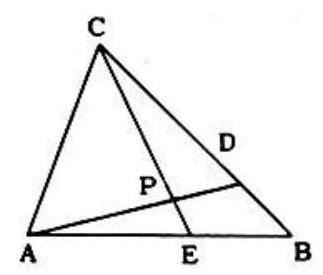
Problem 39: In triangle lines and are drawn so that and . Let where is the intersection point of and . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: If is a number satisfying the equation , then is between:
Answer Choices:
A. 55 and 65
B. 65 and 75
C. 75 and 85
D. 85 and 95
E. 95 and 105
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions