¶ 2025 AMC12B Problems and Solutions
Problem 1: The instructions on a -gram bag of coffee beans say that proper brewing of a large mug of pour-over coffee requires grams of coffee beans. What is the greatest number of properly brewed large mugs of coffee that can be made from the coffee beans in that bag?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Jerry wrote down the ones digit of each of the first positive squares: . What is the sum of all the numbers Jerry wrote down?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What is the value of , where
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The value of the two-digit number in base seven equals the value of the two-digit number in base nine. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Positive integers and satisfy the equation . What is the least possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Emmy says to Max, “I ordered math club sweatshirts today.” Max asks, “How much did each shirt cost?” Emmy responds, “I'll give you a hint. The total cost was , where and are digits and .” After a pause, Max says, “That was a good price.” What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: There are integers and such that the polynomial has as a root. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: What is the tens digit of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The altitude to the hypotenuse of a right triangle is divided into two segments of lengths by the median to the shortest side of the triangle. What is the ratio
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Nine athletes, no two of whom are the same height, try out for the basketball team. One at a time, they draw a wristband at random, without replacement, from a bag containing blue bands, red bands, and green bands. They are divided into a blue group, a red group, and a green group. The tallest member of each group is named the group captain. What is the probability that the group captains are the three tallest athletes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The windshield wiper on the driver's side of a large bus is depicted below.
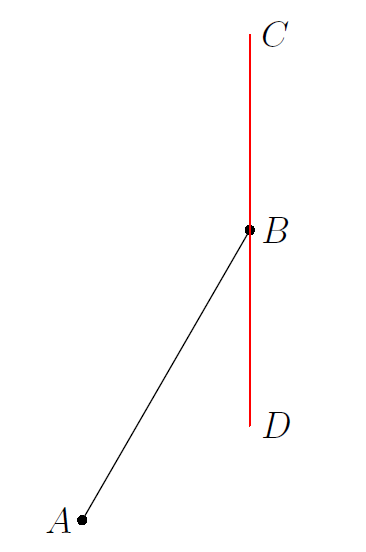
Arm pivots back and forth around point , sweeping out an arc of , symmetric about the vertical line through . The wiper blade is attached to at its midpoint and stays vertical as the arm moves. The arm is feet long, and the wiper blade is feet tall. What is the area of windshield cleaned by the wiper, in square feet, to the nearest hundredth? (Assume that the windshield is a flat vertical surface.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A circle has been divided into sectors of different sizes. Then of the sectors are painted red, painted green, and painted blue so that no two neighboring sectors are painted the same color. One such coloring is shown below.
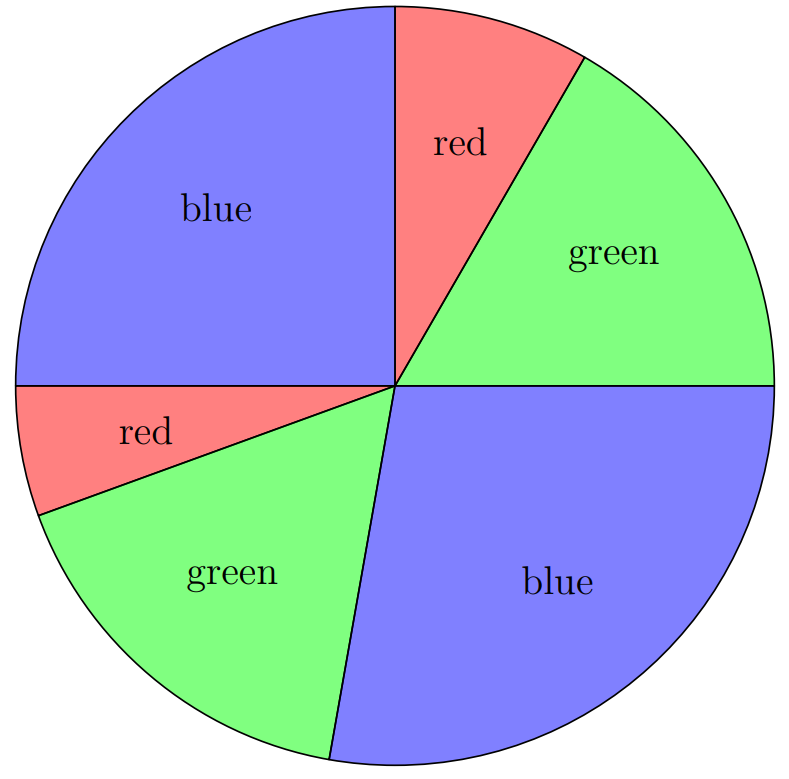
How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Consider a decreasing sequence of positive integers that satisfies:
- The average of the first terms is .
- For all , the average of the first terms is less than the average of the first terms.
What is the greatest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A container has a square bottom, a open square top, and four congruent trapezoidal sides, as shown. Starting when the container is empty, a hose that runs water at a constant rate takes minutes to fill the container up to the midline of the trapezoids.
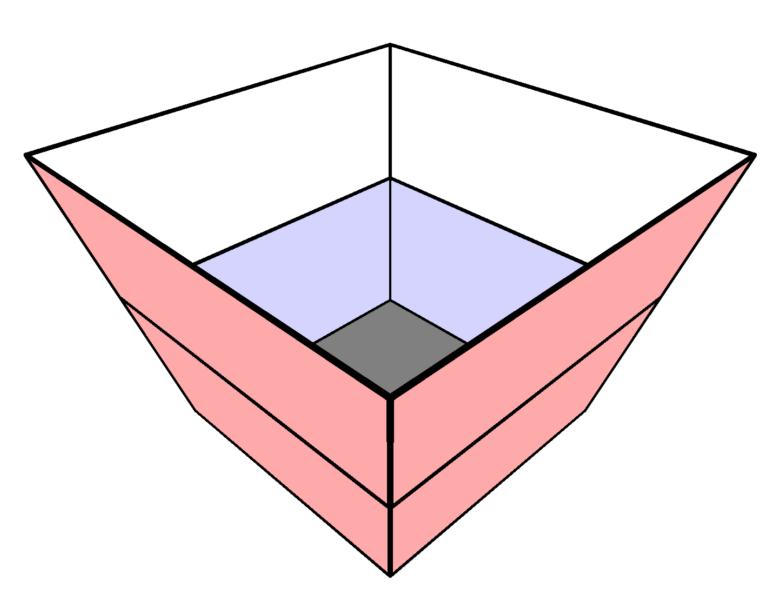
How many more minutes will it take to fill the remainder of the container?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: An analog clock starts at midnight and runs for minutes before stopping. What is the tangent of the acute angle between the hour hand and the minute hand when the clock stops?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Each of the squares in a grid is to be colored red, blue, or yellow in such a way that each red square shares an edge with at least one blue square, each blue square shares an edge with at least one yellow square, and each yellow square shares an edge with at least one red square. Colorings that can be obtained from one another by rotations and/or reflections are considered the same. How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Awnik repeatedly plays a game that has a probability of winning of . The outcomes are independent. What is the expected value of the number of games he will play until he has both won and lost at least once?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A rectangular grid of squares has rows and columns. Each square has room for two numbers. Horace and Vera each fill in the grid with the numbers through . Horace fills horizontally (left to right within each row); Vera fills vertically (top to bottom within each column). How many squares get two copies of the same number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A frog hops along the number line according to the following rules:
- It starts at .
- If it is at , it moves to with probability and disappears with probability .
- For , if it is at , it moves to with probability , to with probability , and disappears with probability .
What is the probability that the frog reaches
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two non-congruent triangles have the same area. Each triangle has sides of length and , and the third side of each triangle has integer length. What is the sum of the lengths of the third sides?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: What is the greatest possible area of the triangle in the complex plane with vertices , , and , where satisfies
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let be the set of all integers such that for all pairs of nonnegative integers with , the remainder when is divided by is less than the remainder when is divided by . What is the sum of the elements of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: How many real numbers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Three concentric circles have radii . An equilateral triangle with side length has one vertex on each circle. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions