¶ 2025 AMC10B Problems and Solutions
Problem 1: The instructions on a -gram bag of coffee beans say that proper brewing of a large mug of pour-over coffee requires grams of coffee beans. What is the greatest number of properly brewed large mugs of coffee that can be made from the coffee beans in that bag?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Jerry wrote down the ones digit of each of the first positive squares: . What is the sum of all the numbers Jerry wrote down?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A Pascal-like triangle has as the top row and followed by as the second row. In each subsequent row the first number is , the last number is , and, as in the standard Pascal Triangle, each other number in the row is the sum of the two numbers directly above it. The first four rows are shown below.
What is the sum of the digits of the sum of the numbers in the th row?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The value of the two-digit number in base seven equals the value of the two-digit number in base nine. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In , , , and . Let be the center of the circle containing points . What is the degree measure of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The line divides the square region defined by and into an upper and a lower region. The line divides the lower region into two regions of equal area. Then can be written as , where and are positive integers. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Frances stands meters directly south of a locked gate in a fence that runs east-west. Immediately behind the fence is a box of chocolates, located meters east of the locked gate. An unlocked gate lies meters east of the box, and another unlocked gate lies meters west of the locked gate. Frances can reach the box by walking toward an unlocked gate, passing through it, and walking toward the box. It happens that the total distance Frances would travel is the same via either unlocked gate. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Emmy says to Max, “I ordered math club sweatshirts today.” Max asks, “How much did each shirt cost?” Emmy responds, “I’ll give you a hint. The total cost was , where and are digits and .” After a pause, Max says, “That was a good price.” What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: How many ordered triples of integers satisfy the following system of inequalities?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Let , and let . What is the sum of all integer values of for which is also an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: On Monday, students went to the tutoring center at the same time, and each one was randomly assigned to one of the tutors on duty. On Tuesday, the same students showed up, the same tutors were on duty, and the students were again randomly assigned to the tutors. What is the probability that exactly students met with the same tutor both Monday and Tuesday?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The figure below shows an equilateral triangle, a rhombus with a angle, and a regular hexagon, each of them containing some mutually tangent congruent disks. Let and respectively, denote the ratio in each case of the total area of the disks to the area of the enclosing polygon. Which of the following is true?
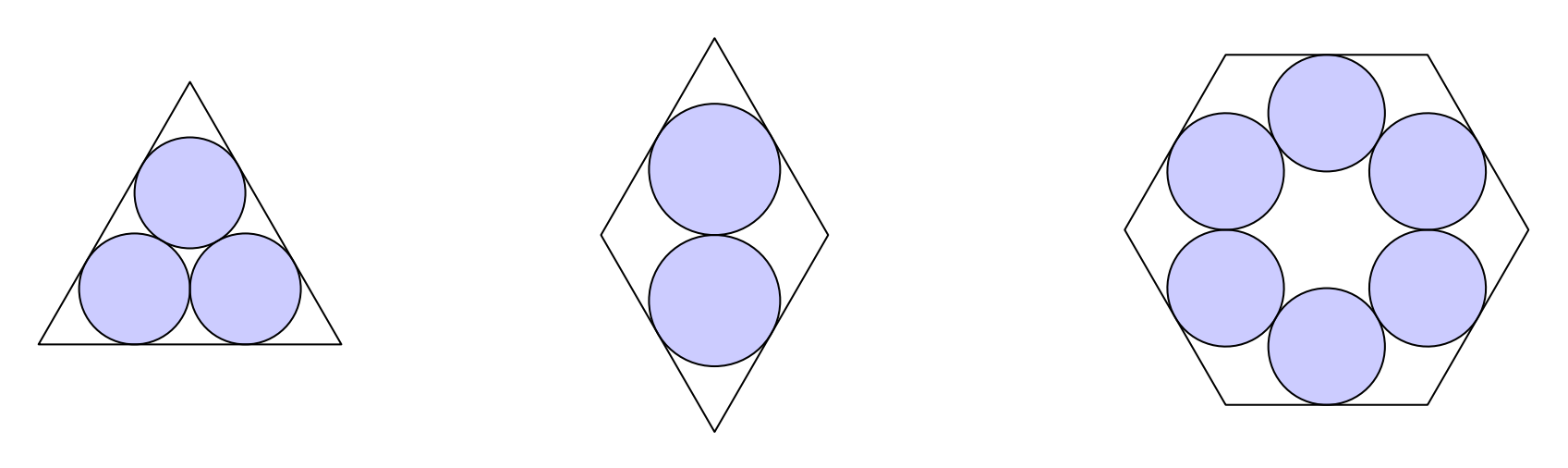
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The altitude to the hypotenuse of a right triangle is divided into two segments of lengths by the median to the shortest side of the triangle. What is the ratio
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Nine athletes, no two of whom are the same height, try out for the basketball team. One at a time, they draw a wristband at random, without replacement, from a bag containing blue bands, red bands, and green bands. They are divided into a blue group, a red group, and a green group. The tallest member of each group is named the group captain. What is the probability that the group captains are the three tallest athletes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The sum can be expressed as , where and are relatively prime positive integers. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A circle has been divided into sectors of different sizes. Then of the sectors are painted red, painted green, and painted blue so that no two neighboring sectors are painted the same color. One such coloring is shown below. How many different colorings are possible?
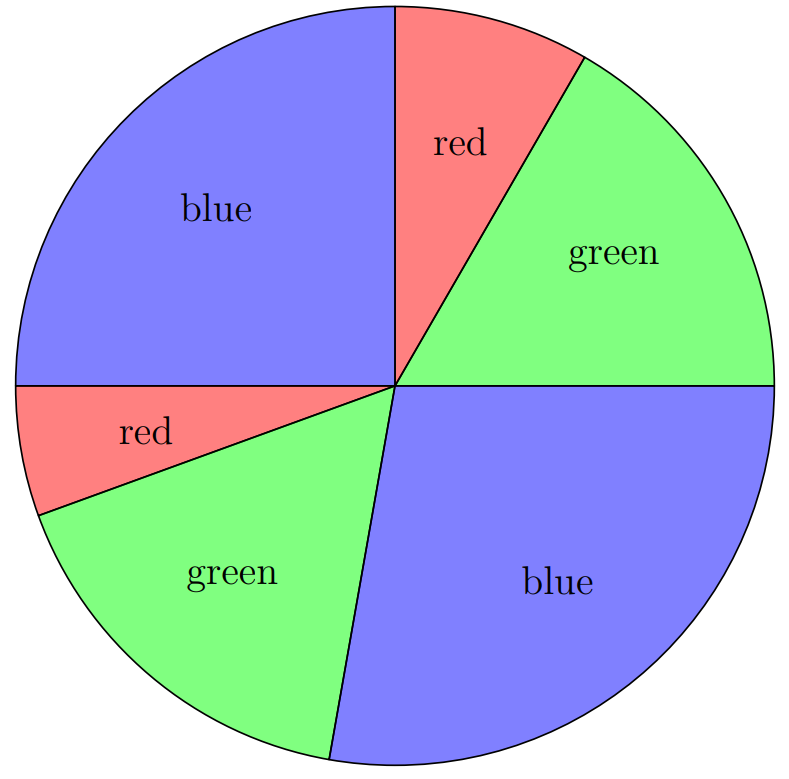
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Consider a decreasing sequence of positive integers that satisfies the following conditions:
- The average of the first terms in the sequence is .
- For all , the average of the first terms is less than the average of the first terms.
What is the greatest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: What is the ones digit of the sum
(Recall that denotes the greatest integer less than or equal to .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A container has a square bottom, a open square top, and four congruent trapezoidal sides, as shown. Starting when the container is empty, a hose that runs water at a constant rate takes minutes to fill the container up to the midline of the trapezoids. How many more minutes will it take to fill the remainder of the container?
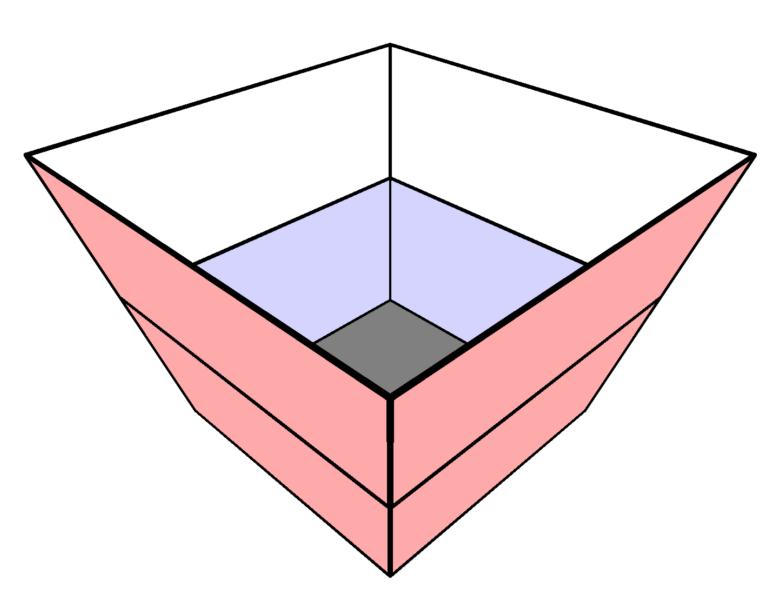
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Four congruent semicircles are inscribed in a square of side length so that their diameters are on the sides of the square, one endpoint of each diameter is at a vertex of the square, and adjacent semicircles are tangent to each other. A small circle centered at the center of the square is tangent to each of the four semicircles, as shown below.
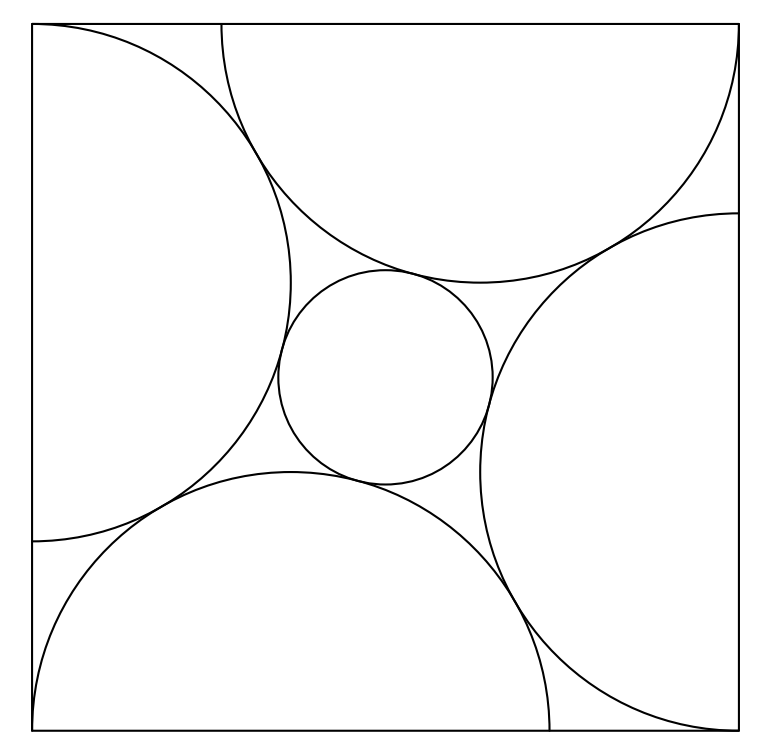
The diameter of the small circle can be written as , where and are integers. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Each of the squares in a grid is to be colored red, blue, or yellow in such a way that each red square shares an edge with at least one blue square, each blue square shares an edge with at least one yellow square, and each yellow square shares an edge with at least one red square. Colorings that can be obtained from one another by rotations and/or reflections are considered the same. How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A seven-digit positive integer is chosen at random. What is the probability that the number is divisible by , given that the sum of its digits is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A rectangular grid of squares has rows and columns. Each square has room for two numbers. Horace and Vera each fill in the grid by putting the numbers from through into the squares. Horace fills the grid horizontally: he puts through left to right in row , through in row , and so on. Vera fills the grid vertically: she puts through top to bottom into column , then through into column , and so on. How many squares get two copies of the same number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A frog hops along the number line according to the following rules:
- It starts at .
- If it is at , then it moves to with probability and disappears with probability .
- For , if it is at , then it moves to with probability , to with probability , and disappears with probability .
What is the probability that the frog reaches
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Square has sides of length . Points and lie on and , respectively, with and . A path begins along the segment from to and continues by reflecting against the sides of (with congruent incoming and outgoing angles). If the path hits a vertex of the square, it terminates there; otherwise it continues forever. At which vertex does the path terminate?
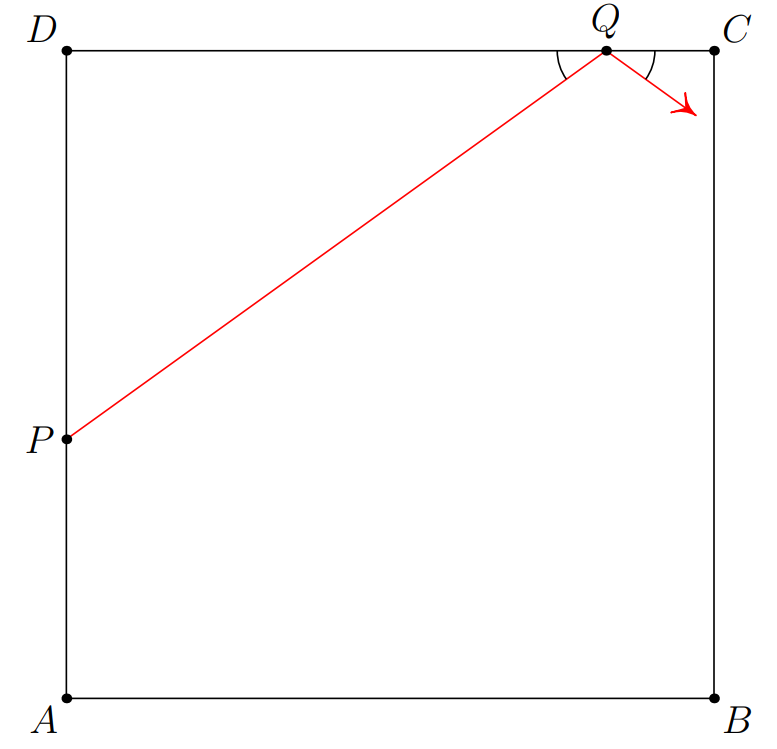
Answer Choices:
A.
B.
C.
D.
E. The path continues forever
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions