¶ 2025 AMC10A Problems and Solutions
Problem 1: Andy and Betsy both live in Mathville. Andy leaves Mathville on his bicycle at , traveling due north at a steady miles per hour. Betsy leaves on her bicycle from the same point at , traveling due east at a steady miles per hour. At what time will they be exactly the same distance from their common starting point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A box contains pounds of a nut mix that is percent peanuts, percent cashews, and percent almonds. A second nut mix containing percent peanuts, percent cashews, and percent almonds is added to the box resulting in a new nut mix that is percent peanuts. How many pounds of cashews are now in the box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many isosceles triangles are there with positive area whose side lengths are all positive integers and whose longest side has length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A team of students is going to compete against a team of teachers in a trivia contest. The total number of students and teachers is . Ash, a cousin of one of the students, wants to join the contest. If Ash plays with the students, the average age on that team will increase from to . If Ash plays with the teachers, the average age on that team will decrease from to . How old is Ash?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Consider the sequence of positive integers
What is the term in this sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In an equilateral triangle each interior angle is trisected by a pair of rays. The intersection of the interiors of the middle -angle at each vertex is the interior of a convex hexagon. What is the degree measure of the smallest angle of this hexagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Suppose and are real numbers. When the polynomial is divided by , the remainder is . When the polynomial is divided by , the remainder is . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Agnes writes the following four statements on a blank piece of paper.
- At least one of these statements is true.
- At least two of these statements are true.
- At least two of these statements are false.
- At least one of these statements is false.
Each statement is either true or false. How many false statements did Agnes write on the paper?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Let For how many real numbers does the graph of pass through the point
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 10: A semicircle has diameter and chord of length parallel to . A smaller semicircle with diameter on and tangent to is cut from the larger semicircle, as shown below.
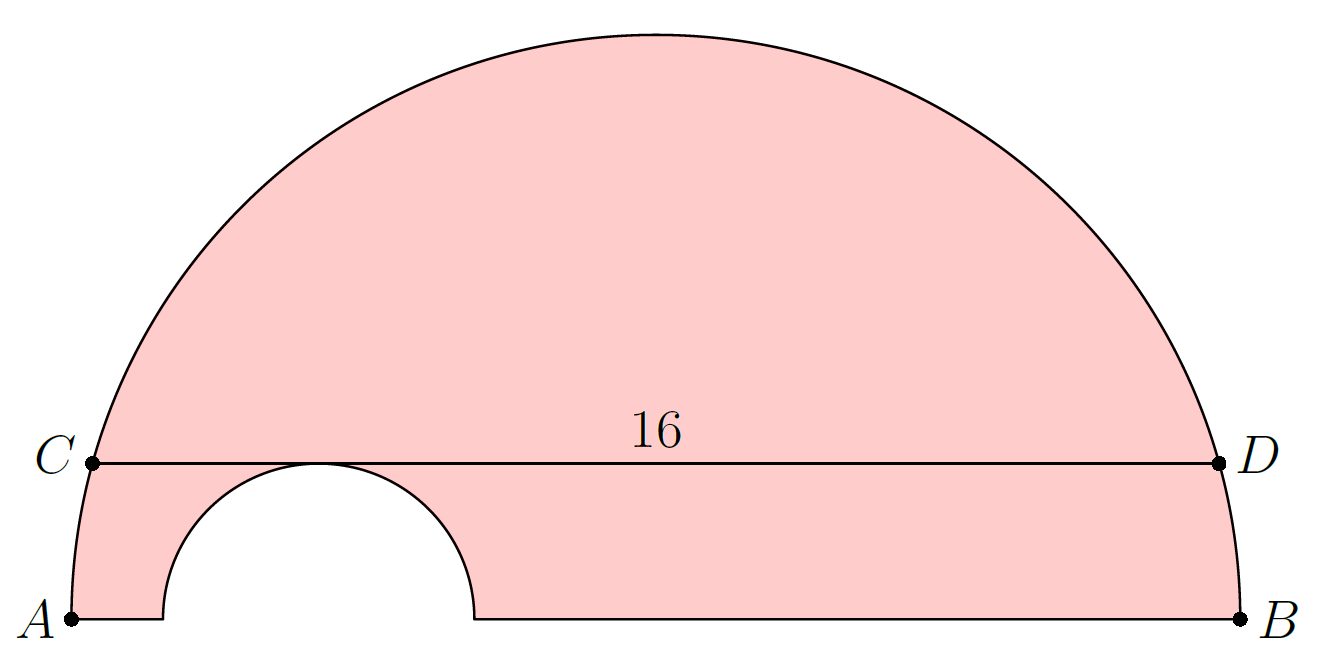
What is the area of the resulting figure, shown shaded?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The sequence is arithmetic. The sequence is geometric. Both sequences are strictly increasing and contain only integers, and is as small as possible. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Carlos uses a -digit passcode to unlock his computer. In his passcode, exactly one digit is even, exactly one (possibly different) digit is prime, and no digit is . How many -digit passcodes satisfy these conditions?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In the figure below, the outside square contains infinitely many squares, each of them with the same center and sides parallel to the outside square. The ratio of the side length of a square to the side length of the next inner square is , where . The spaces between squares are alternately shaded, as shown in the figure (which is not necessarily drawn to scale).

The area of the shaded portion of the figure is of the area of the original square. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Six chairs are arranged around a round table. Two students and two teachers randomly select four of the chairs to sit in. What is the probability that the two students will sit in two adjacent chairs and the two teachers will also sit in two adjacent chairs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In the figure below, is a rectangle, , , , and
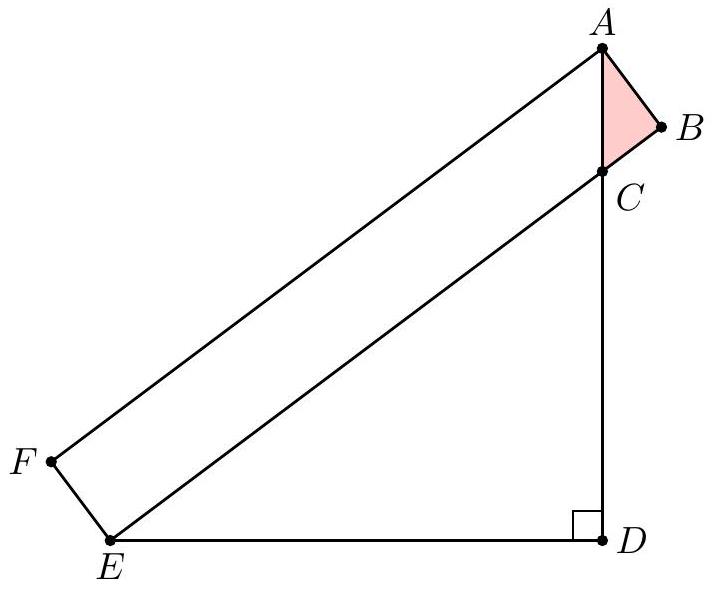
What is the area of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: There are three jars. Each of three coins is placed in one of the three jars, chosen at random and independently of the placements of the other coins. What is the expected number of coins in a jar with the most coins?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be the unique positive integer such that dividing by leaves a remainder of and dividing by leaves a remainder of . What is the tens digit of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The harmonic mean of a collection of numbers is the reciprocal of the arithmetic mean of the reciprocals of the numbers in the collection. For example, the harmonic mean of is
What is the harmonic mean of all the real roots of the degree polynomial
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: An array of numbers is constructed beginning with the numbers in the top row. Each adjacent pair of numbers is summed to produce a number in the next row. Each row begins and ends with and , respectively.
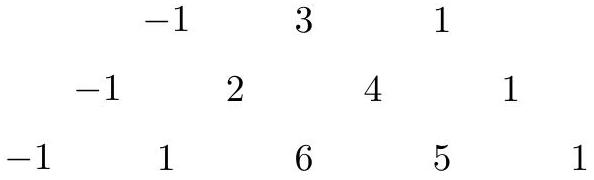
If the process continues, one of the rows will sum to In that row, what is the third number from the left?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A silo (right circular cylinder) with diameter meters stands in a field. MacDonald is located meters west and meters south of the center of the silo. McGregor is located meters east and meters south of the center of the silo. The line of sight between MacDonald and McGregor is tangent to the silo. The value of can be written as , where are positive integers, is not divisible by the square of any prime, and is relatively prime to . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A set of numbers is called sum-free if whenever and are (not necessarily distinct) elements of the set, is not an element of the set. For example, and the empty set are sum-free, but is not. What is the greatest possible number of elements in a sum-free subset of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A circle of radius is surrounded by three circles, whose radii are and all externally tangent to the inner circle and to each other, as shown.
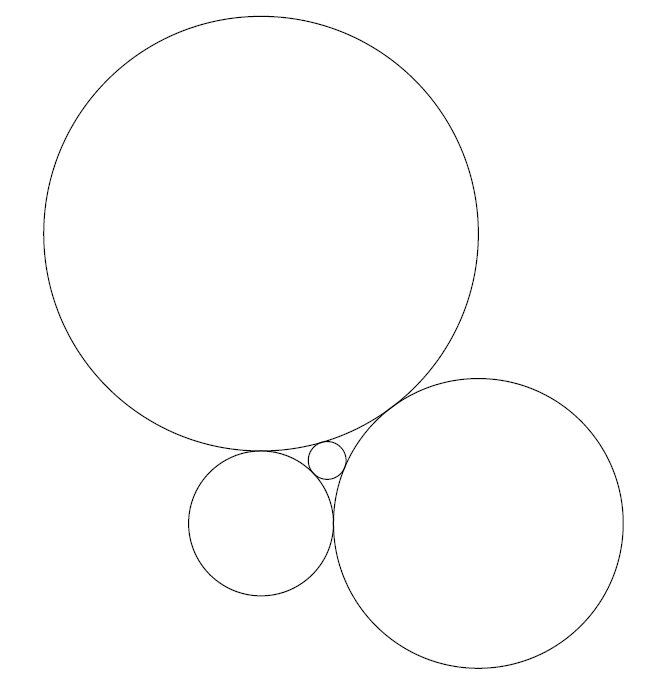
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Triangle has side lengths , , and . The bisector of and the altitude to side intersect at point What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Call a positive integer fair if no digit is used more than once, it has no s, and no digit is adjacent to two greater digits. For example, , and are fair, but , and are not. How many fair positive integers are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A point is chosen at random inside square The probability that is neither the shortest nor the longest side of can be written as , where are positive integers, and is not divisible by the square of any prime. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions